The mass of .73Li is 0.042 amu less than the sum of masses of its constituents. The binding energy per nucleon is
5.586 MeV
10.522 MeV
2.433 MeV
3.739 MeV
The correct Answer is:a
To find the binding energy per nucleon for the lithium-7 nucleus (Li-7), we will follow these steps:
Step 1: Understand the mass defect
The mass defect (ΔM) is given as 0.042 amu. This is the difference between the sum of the masses of the individual nucleons (protons and neutrons) and the actual mass of the nucleus.
Step 2: Convert mass defect to energy
The binding energy (BE) can be calculated using the mass defect and Einstein's mass-energy equivalence principle. The formula to convert mass defect in amu to energy in MeV is:
BE=ΔM×931.5 MeV/amu
Substituting the given mass defect:
BE=0.042 amu×931.5 MeV/amu
Step 3: Calculate the total binding energy
Now, we perform the multiplication:
BE=0.042×931.5≈39.1 MeV
Step 4: Determine the binding energy per nucleon
The binding energy per nucleon is calculated by dividing the total binding energy by the mass number (A) of the nucleus. For lithium-7, the mass number A=7.
BEper nucleon=BEA=39.1 MeV7
Step 5: Perform the final calculation
Now we calculate the binding energy per nucleon:
BEper nucleon≈39.17≈5.586 MeV
Conclusion
The binding energy per nucleon for lithium-7 is approximately 5.586 MeV.
---
The mass defect (ΔM) is given as 0.042 amu. This is the difference between the sum of the masses of the individual nucleons (protons and neutrons) and the actual mass of the nucleus.
The binding energy (BE) can be calculated using the mass defect and Einstein's mass-energy equivalence principle. The formula to convert mass defect in amu to energy in MeV is:
Now, we perform the multiplication:
The binding energy per nucleon is calculated by dividing the total binding energy by the mass number (A) of the nucleus. For lithium-7, the mass number A=7.
Now we calculate the binding energy per nucleon:
The binding energy per nucleon for lithium-7 is approximately 5.586 MeV.
Topper's Solved these Questions
- NUCLEIBook:NCERT FINGERTPS ENGLISHChapter:NUCLEIExercise:HOTS
Explore 7 Videos
- NUCLEIBook:NCERT FINGERTPS ENGLISHChapter:NUCLEIExercise:EXEMPLAR PROBLEMS
Explore 7 Videos
- MOVING CHARGES AND MAGNETISM Book:NCERT FINGERTPS ENGLISHChapter:MOVING CHARGES AND MAGNETISM Exercise:Assertion And Reason
Explore 15 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Paper 3
Explore 50 Videos
Similar Questions
As the mass number A increases, the binding energy per nucleon in a nucleus.
View SolutionThe mass of a H-atom is less than the sum of the masses of a proton and electron. Why is this?
View SolutionThe actual atomic mass of .20Ca40 is 39.96259 amu. Find the binding energy for this nuclide, using 1.008665 amu for the mass of a neutron and 1.007825 amu for the mass of atomic hydrogen. Also calculate the binding energy per nucleon.
View Solution(a) The mass of a nucleus in its ground state is always less than total mass of its constituents - neutrons and protons. Explain.
(b) Plot a graph showing the variation of potential energy of a pair of nucleons as a function of their separation.
View SolutionThe source of energy of stars is nuclear fusion. Fusion reaction occurs at very high temperature, about 107. Energy released in the process of fusion is due to mass defect. It is also called Q-value. Q=Δmc2,Δm= mass defect.
The binding energy per nucleon of .1H2 and .2He4 are 1.1MeV and 7MeV, respectively. If two deuteron nuclei react to form a single helium nucleus, then the energy released is
View SolutionAssertion: The nuclear energy can be obtained by the nuclear fission of heavier nuclei as well as by fusion of lighter nuclei.
Reason: As the mass number increases, the binding energy per nucleon, first increases and then decreases.
View SolutionAtomic mass of .136C is 13.00335 amu and its mass number is 13.0. If 1 amu = 931 MeV. binding energy of the neutrons present in the nucleus is
View SolutionThe mass defect for the nucleus of helium is 0.0303 a.m.u. What is the binding energy per nucleon for helium in MeV ?
View SolutionDraw the graph showing thervariation of binding energy per nucleon with mass number. Give therason for the decrease of binding energy per nucleon for nuclei with high mass numbers.
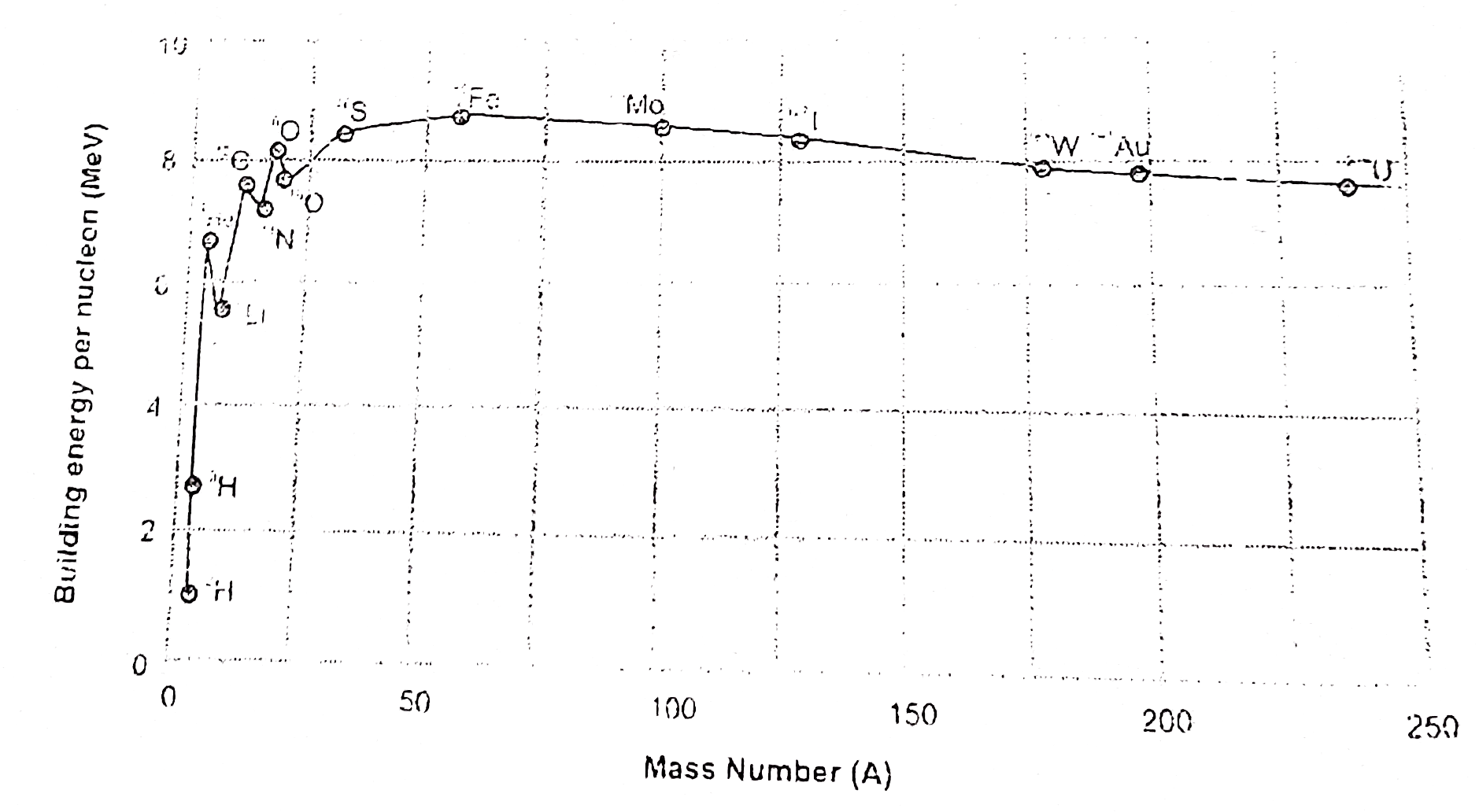
The binding energy per nucleon for nuclei with high mass number is low due to the large coulomb repulsion between the protons inside these nuclei.
View SolutionAll nuclei consist of two types of particles- protaon and neutrons. Nuclear force is the strongest froce. Stability of nucleus is determined by the neutron - proton ratio or mass defect or binding energy per nucleus or packing fraction. Shape of nucleus is calculated by quadrupole moment. Spin of nucleus depends on even or odd mass number. Volume of nucleus depends on the mass number. Whole mass of the atom (nearly 99%) is centered at the nucleus. Magnetic moment of the nucleus is measured in terms of the nuclear magnetons.
Binding energy per nucleon is maximum.
View Solution

