The ratio of the nuclear radii of the gold isotope .19779Au and silver isotope .10747Ag is
1.23
0.216
2.13
3.46
The correct Answer is:a
To find the ratio of the nuclear radii of the gold isotope 19779Au and the silver isotope 10747Ag, we can use the formula for nuclear radius:
R=R0⋅A1/3
where R0 is a constant (approximately 1.2fm) and A is the mass number of the nucleus.
Step 1: Identify the mass numbers
- For gold 19779Au, the mass number AAu=197.
- For silver 10747Ag, the mass number AAg=107.
Step 2: Write the formula for the nuclear radii
The nuclear radius for gold can be expressed as:
RAu=R0⋅(197)1/3
The nuclear radius for silver can be expressed as:
RAg=R0⋅(107)1/3
Step 3: Calculate the ratio of the nuclear radii
The ratio of the nuclear radii RAuRAg is given by:
RAuRAg=R0⋅(197)1/3R0⋅(107)1/3=(197)1/3(107)1/3
Step 4: Simplify the ratio
This simplifies to:
RAuRAg=(197107)1/3
Step 5: Calculate the numerical value
Now we can calculate 197107:
197107≈1.8383
Taking the cube root:
(1.8383)1/3≈1.220
Conclusion
Thus, the ratio of the nuclear radii of the gold isotope to the silver isotope is approximately:
RAuRAg≈1.22
Final Answer
The ratio of the nuclear radii of the gold isotope 19779Au and silver isotope 10747Ag is approximately 1.22.
---
- For gold 19779Au, the mass number AAu=197.
- For silver 10747Ag, the mass number AAg=107.
The nuclear radius for gold can be expressed as:
RAu=R0⋅(197)1/3
The nuclear radius for silver can be expressed as:
RAg=R0⋅(107)1/3
The ratio of the nuclear radii RAuRAg is given by:
RAuRAg=R0⋅(197)1/3R0⋅(107)1/3=(197)1/3(107)1/3
This simplifies to:
RAuRAg=(197107)1/3
Now we can calculate 197107:
197107≈1.8383
Taking the cube root:
(1.8383)1/3≈1.220
Thus, the ratio of the nuclear radii of the gold isotope to the silver isotope is approximately:
RAuRAg≈1.22
The ratio of the nuclear radii of the gold isotope 19779Au and silver isotope 10747Ag is approximately 1.22.
Topper's Solved these Questions
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - HOTS
7 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - EXEMPLAR PROBLEMS
7 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
Similar Questions
Obtain approx. the ratio of the nuclear radii of the gold isotope .79Au197 and silver isotope .47Ag107.
View SolutionObtain approx. the ratio of the nuclear radii of the gold isotope .79Au197 and silver isotope .47Ag107.
View SolutionRatio of nuclear radii of 135Csto40Ca is
View SolutionIf two deuterium nuclei get close enough to each other, the attraction of the strong nuclear force will fuse them to make an isotope of helium. This process releases a huge amount of energy. The range of nuclear force is 10−15 m. This is the principle behind the nuclear fusion reactor. The deuterium nuclei moves to fast that, it is not possible to contain them by physical walls. Therefore they are confined magnetically (Assume coulomb law to hold even at 10−18 m)
Two deuterium nuclei having same speed undergo a head on collision. Which of the following is closest to the minimum value of v (in km/sec) for which fusion occurs
View SolutionWhich of the following nuclear reactions will generate an isotope ?
View SolutionUranium ores on the earth at the present time typically have a composition consisting of 99.3% of the isotope .92U238 and 0.7% of the isotope .92U235. The half-lives of these isotopes are 4.47×109yr and 7.04×108yr, respectively. If these isotopes were equally abundant when the earth was formed, estimate the age of the earth.
View SolutionUranium ores on the earth at the present time typically have a composition consisting of 99.3% of the isotope _92U238 and 0.7% of the isotope _92U235. The half-lives of these isotopes are 4.47×109yr and 7.04×108yr, respectively. If these isotopes were equally abundant when the earth was formed, estimate the age of the earth.
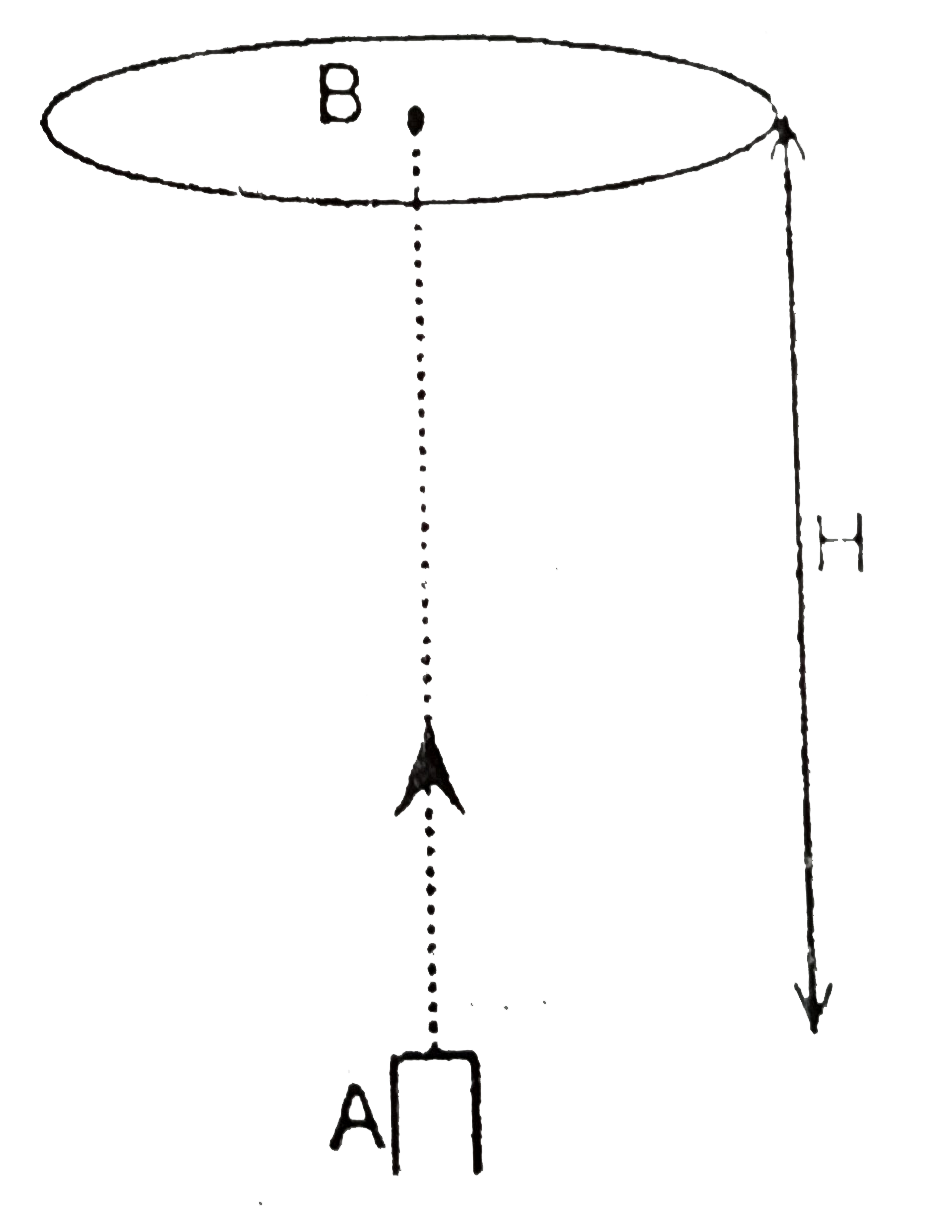
View SolutionThere is uniformly charged disc of surface charge density σ and of radius 1m. H=10m height below the disc is a gun which is continuously emitting a charged particle and its isotopic in the vertically upward direction. The particles are charged through same potential before being emitted. The charge of the particle is q=8×10−19C. The difference of potential energies of particle and the isotopic at B is 10−23Joule. Also the velocity of the particle at B is zero. The ratio of masses of particle and isotopic is 32. If the total energy of isotope at B is 1.1k×10−23J Then find k..(Given σ/ε0=10−4N/C).
View SolutionWhen n/p ratio of an isotope is greater than the stable isotope of that element, it emits
View SolutionIn the chemical analysis of a rock the mass ratio of two radioactive isotopes is found to be 100:1. The mean lives of the two isotopes are 4×109 years and 2×109 years, respectively. If it is assumed that at the time of formation the atoms of both the isotopes were in equal propotional, calculate the age of the rock. Ratio of the atomic weights of the two isotopes is 1.02:1.
View Solution
