A 2 m long solenoil with diameter 2 cm and 2000 turns has a secondary coil of 1000 turns wound closely near its midpoint. The mutuat inductance between the two coils is.
2.4×10−4H
3.9×10−4H
1.28×10−3H
3.14×10−3H
The correct Answer is:B
To solve the problem of finding the mutual inductance between the solenoid and the secondary coil, we can follow these steps:
Step 1: Identify the given values
- Length of the solenoid (L) = 2 m
- Diameter of the solenoid (D) = 2 cm = 0.02 m
- Radius of the solenoid (r) = D/2 = 0.01 m
- Number of turns in the primary coil (N1) = 2000 turns
- Number of turns in the secondary coil (N2) = 1000 turns
Step 2: Calculate the cross-sectional area (A) of the solenoid
The area A of the solenoid can be calculated using the formula for the area of a circle:
A=πr2
Substituting the radius:
A=π(0.01)2=π×10−4 m2
Step 3: Use the formula for mutual inductance (M)
The formula for mutual inductance between two coils is given by:
M=μ0N1N2AL
Where:
- μ0 (permeability of free space) = 4π×10−7 H/m
- N1 = number of turns in the primary coil
- N2 = number of turns in the secondary coil
- A = cross-sectional area
- L = length of the solenoid
Step 4: Substitute the values into the formula
Substituting the known values into the formula:
M=(4π×10−7)×2000×1000×(π×10−4)2
Step 5: Simplify the expression
Calculating the above expression:
M=(4π×10−7)×2000×1000×π×10−42
=4×2000×1000×π2×10−112
=2×2000×1000×π2×10−11
=3.9×10−4 H
Final Answer
The mutual inductance M between the two coils is:
M≈3.9×10−4 Henry
- Length of the solenoid (L) = 2 m
- Diameter of the solenoid (D) = 2 cm = 0.02 m
- Radius of the solenoid (r) = D/2 = 0.01 m
- Number of turns in the primary coil (N1) = 2000 turns
- Number of turns in the secondary coil (N2) = 1000 turns
The area A of the solenoid can be calculated using the formula for the area of a circle:
A=πr2
Substituting the radius:
A=π(0.01)2=π×10−4 m2
The formula for mutual inductance between two coils is given by:
M=μ0N1N2AL
Where:
- μ0 (permeability of free space) = 4π×10−7 H/m
- N1 = number of turns in the primary coil
- N2 = number of turns in the secondary coil
- A = cross-sectional area
- L = length of the solenoid
Substituting the known values into the formula:
M=(4π×10−7)×2000×1000×(π×10−4)2
Calculating the above expression:
M=(4π×10−7)×2000×1000×π×10−42
=4×2000×1000×π2×10−112
=2×2000×1000×π2×10−11
=3.9×10−4 H
The mutual inductance M between the two coils is:
M≈3.9×10−4 Henry
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION AND REASON
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
If a current of 3.0 amperes flowing in the primary coil is reduced to zero in 0.001 second, then the induced e.m.f. in the secondary coil is 15000volts. The mutual inductance between the two coils is
View SolutionA solenoid is of length 50 cm and has a radius of 2cm. It has 500 turns. Around its central section a coil of 50 turns is wound. Calculate the mutual inductance of the system.
View Solution
Knowledge Check
When the number of turns in the two circular coils closely wound are doubled (in both) their mutual inductance becomes
Abecomes 4 timesBbecomes 2 timesCbecomes 14 timesDremains unchanged
A long solenoid of length L, cross section A having N1 turns has about its center a small coil of N2 turns as shows in Fig The mutual inductance of two circuits is
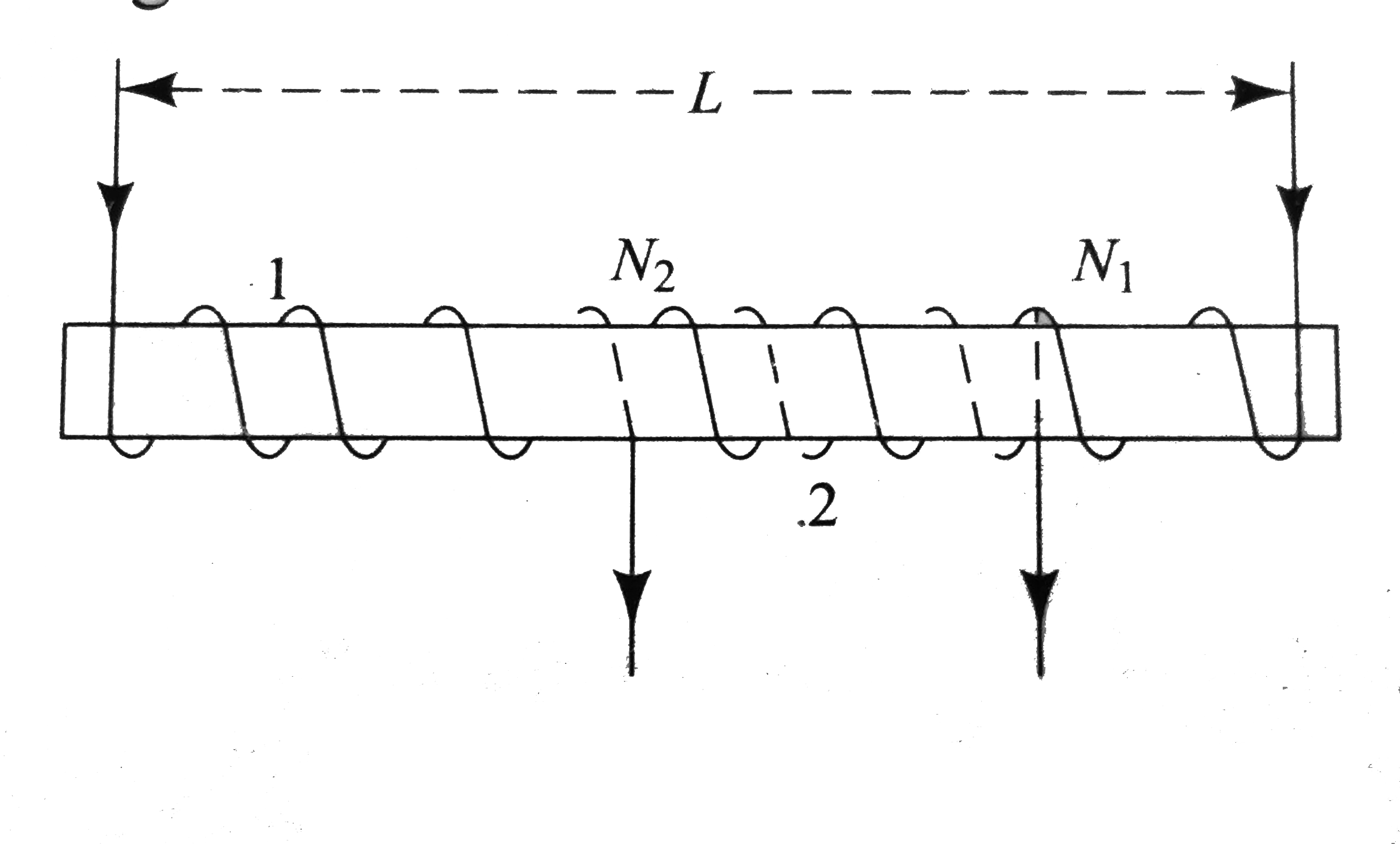
View SolutionA current l = 1.5 A is flowing through a long solenoid of diameter 3.2 cm, having 220 turns per cm. At its centre, a 130 turn closely packed coil of diameter 2.1 cm is placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 25 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View SolutionOver a solenoid of 50cm length and 2cm radius and having 500turns is would another wire of 50 turns near the centre. Calculate
(i) mutual inductance of the two coils
(ii) Induced emf in the second coil when the current in the primary changes from 0 to 5A in 0.02 sec.
View SolutionWith the decrease of current in the primary coil from 2 amperes to zero value in 0.01 s the emf generated in the secondary coil is 1000 volts. The mutual inductance of the two coils is
View SolutionIf number of turns in primary and secondary coils is increased to two times each, the mutual inductance
View SolutionIf the current in the primary circuit of a pair of coils changes from 5 amp to 1 amp in 0.02 sec, calculate (i) induced emf in the secondary coil if the mutual inductance between the two coils is 0.5H and (ii) the change of flux per turn in the secondary, if it has 200 turns.
View SolutionA straight solenoid of length 1m has 5000 turns in the primary and 200 turns in the secondary. If the area of cross section is 4cm2, the mutual inductance will be
View Solution
