Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once, calling the loop as C, which of the option is correct ?
the value of is independent of sense of C.
there may be a point on C where B and dl are parallel.
none of these
The correct Answer is:B
To solve the problem regarding two identical coaxial loops carrying current in opposite directions, we will follow these steps:
Step 1: Understand the Setup
We have two identical coaxial loops. Let’s denote them as Loop 1 and Loop 2. Loop 1 carries a current I in an anticlockwise direction, while Loop 2 carries the same current I in a clockwise direction.
Step 2: Define the Amperian Loop
We consider an Amperian loop C that passes through both loops. This loop is an imaginary closed path used to apply Ampere's circuital law.
Step 3: Apply Ampere's Circuital Law
According to Ampere's circuital law:
∮B⋅dl=μ0Ienc
where Ienc is the net current enclosed by the Amperian loop.
Step 4: Determine the Enclosed Current
Since Loop 1 carries current I in one direction and Loop 2 carries current I in the opposite direction, the net current enclosed by the Amperian loop C is:
Ienc=I−I=0
Step 5: Calculate the Line Integral
Substituting Ienc=0 into Ampere's law gives:
∮B⋅dl=μ0⋅0=0
This implies that:
∮B⋅dl=0
Step 6: Analyze the Options
Now, we need to analyze the given options based on our findings:
- Option A states that ∮B⋅dl=±2μ0, which is incorrect since we found it to be 0.
- Option B states that the value of ∮B⋅dl is independent of the sense of current, which is correct because regardless of the direction of the currents, the net current is still zero.
- Option C suggests there exists a point on C where B and dl are parallel, which is incorrect as the magnetic fields from both loops cancel each other out.
- Option D states that none of the above options are correct, which is also incorrect since Option B is correct.
Conclusion
The correct answer is Option B.
---
We have two identical coaxial loops. Let’s denote them as Loop 1 and Loop 2. Loop 1 carries a current I in an anticlockwise direction, while Loop 2 carries the same current I in a clockwise direction.
We consider an Amperian loop C that passes through both loops. This loop is an imaginary closed path used to apply Ampere's circuital law.
According to Ampere's circuital law:
∮B⋅dl=μ0Ienc
where Ienc is the net current enclosed by the Amperian loop.
Since Loop 1 carries current I in one direction and Loop 2 carries current I in the opposite direction, the net current enclosed by the Amperian loop C is:
Ienc=I−I=0
Substituting Ienc=0 into Ampere's law gives:
∮B⋅dl=μ0⋅0=0
This implies that:
∮B⋅dl=0
Now, we need to analyze the given options based on our findings:
- Option A states that ∮B⋅dl=±2μ0, which is incorrect since we found it to be 0.
- Option B states that the value of ∮B⋅dl is independent of the sense of current, which is correct because regardless of the direction of the currents, the net current is still zero.
- Option C suggests there exists a point on C where B and dl are parallel, which is incorrect as the magnetic fields from both loops cancel each other out.
- Option D states that none of the above options are correct, which is also incorrect since Option B is correct.
The correct answer is Option B.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM Book:NCERT FINGERTPS ENGLISHChapter:MOVING CHARGES AND MAGNETISM Exercise:HOTS
Explore 5 Videos
- MOVING CHARGES AND MAGNETISM Book:NCERT FINGERTPS ENGLISHChapter:MOVING CHARGES AND MAGNETISM Exercise:EXEMPLAR PROBLEMS
Explore 6 Videos
- MAGNETISM AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:MAGNETISM AND MATTER Exercise:NCERT Exemplar
Explore 5 Videos
- NUCLEIBook:NCERT FINGERTPS ENGLISHChapter:NUCLEIExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Knowledge Check
Two circular, similar, coaxial loops carry equal currents in the same direction. If the loops are brought nearer, what will happen?
AP increases while in Q decreasesBQ increases while in P decreasesCboth P and Q increasesDboth P and Q decreases
Two circular, similar, coaxial loops carry equal currents in the same direction. If the loops are brought nearer, what will happen?
View SolutionA current carrying loop in a uniform magnetic field will experience
View SolutionA current carrying loop lies on a smooth horizontal plane. Then,
View SolutionMagnetic moment of a current carrying square loop be M. If it is converted in form of circle and same current is passed through it then find the new magnetic moment.
View SolutionMagnetic moment of a current carrying square loop be M. If it is converted in form of circle and same current is passed through it then find the new magnetic moment.
View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
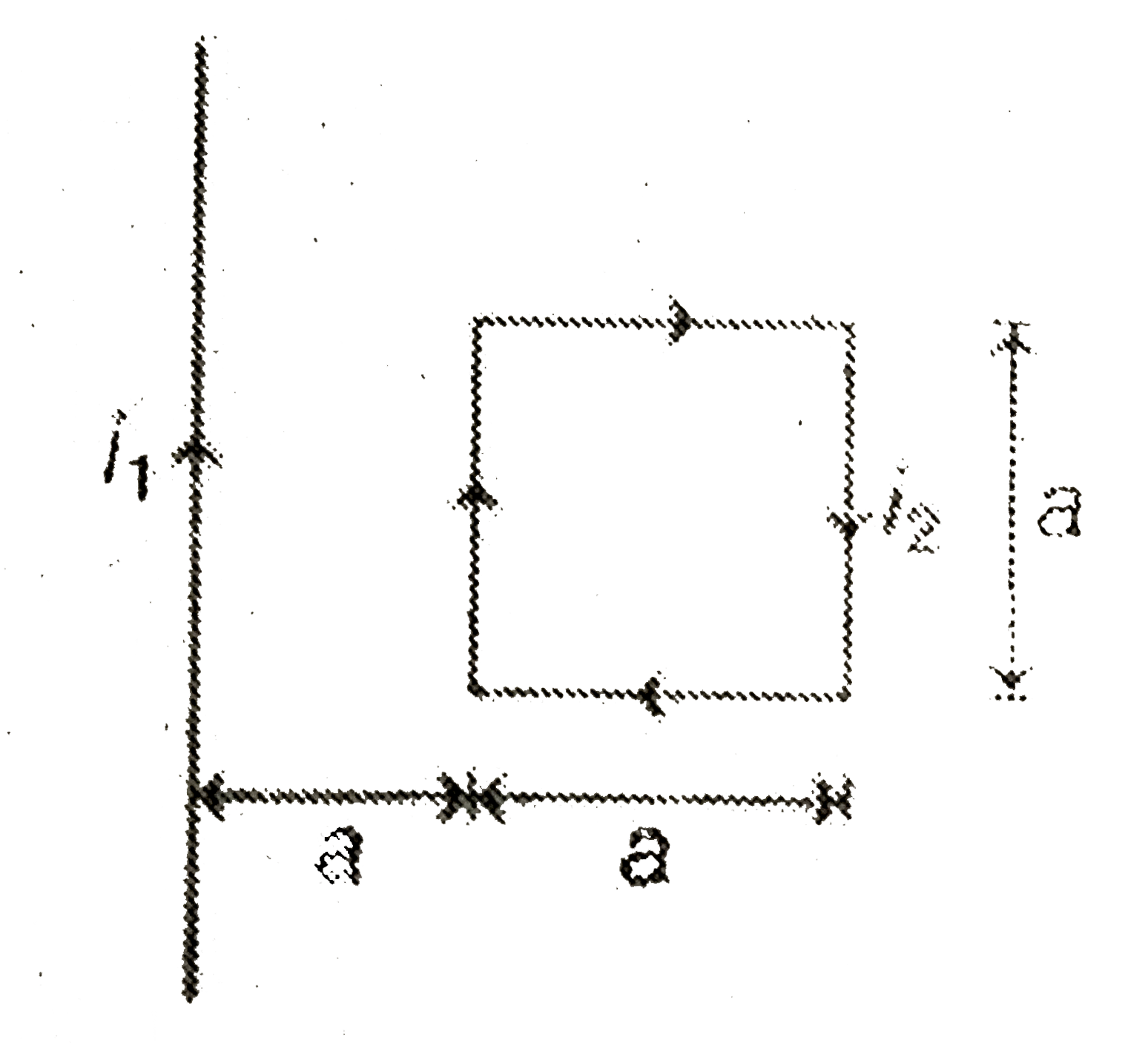
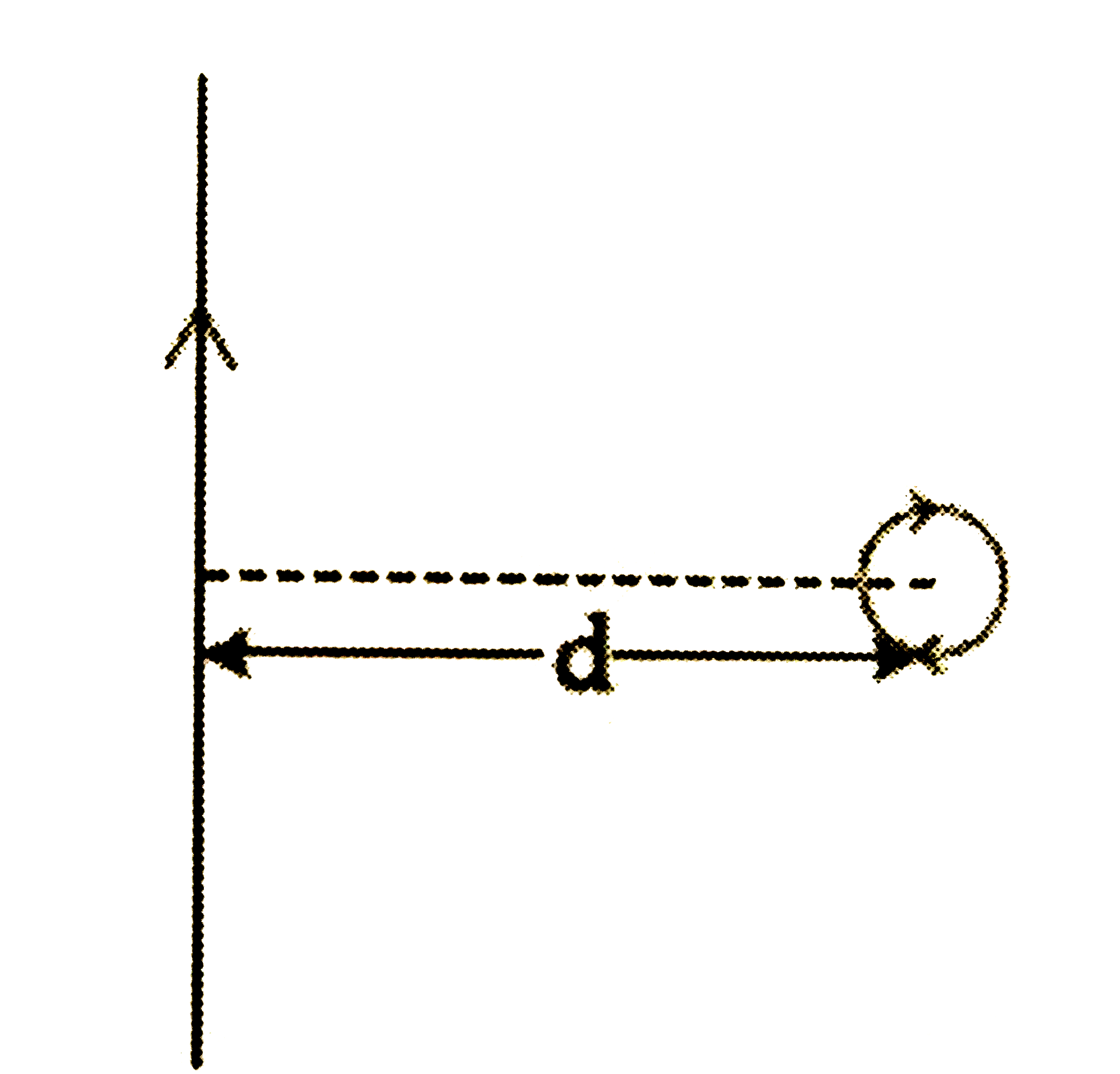
View SolutionAn infinitely long current carrying wire and a small current carrying loop are in the plane of the paper as shown. The radius of the loop is a and distance of its centre from the wire is d (d>>a). If the loop applies a force F on the wire then :
View Solution


