A cubical region of space is filled with some uniform electric and magnetic field. An electron enters the cube across one of its faces with velocity v and a positron enters via opposite face with velocity- v. At this instant, which one of the following is not correct?
The electric forces on both the particles cause identical acceleration.
The magnetic forces on both the particles cause equal acceleration.
Both particles gain or loose energy at the same rate.
The motion of the centre of mass is determined by B alone.
The correct Answer is:A
To solve the problem step by step, we will analyze the situation involving the electron and positron entering a cubical region filled with uniform electric and magnetic fields.
1. Identify the Charges and Velocities:
- An electron enters the cube with velocity v.
- A positron enters the cube with velocity −v.
- The charges are −e for the electron and +e for the positron.
2. Calculate the Electric Force on Each Particle:
- The electric force on the electron is given by:
Fe=−eE
- The electric force on the positron is given by:
Fp=+eE
- The accelerations can be calculated using F=ma:
- For the electron:
ae=−eEm
- For the positron:
ap=+eEm
3. Compare the Accelerations:
- Since ae and ap have opposite signs, they are not identical. Thus, the statement that "the electric force on both the particles causes identical acceleration" is incorrect.
4. Calculate the Magnetic Force on Each Particle:
- The magnetic force on the electron is given by:
FBe=−e(v×B)
- The magnetic force on the positron is given by:
FBp=+e(−v×B)=−e(−v×B)=e(v×B)
- The corresponding accelerations are:
- For the electron:
aBe=−e(v×B)m
- For the positron:
aBp=e(v×B)m
5. Compare the Magnetic Accelerations:
- The magnitudes of the magnetic forces are equal, thus the accelerations due to the magnetic force are equal in magnitude but opposite in direction. Therefore, the statement that "the magnetic force on both the particles causes equal acceleration" is correct.
6. Energy Gain or Loss:
- Both particles have the same charge magnitude and mass. Therefore, they gain or lose energy at the same rate when subjected to the same electric and magnetic fields. This statement is correct.
7. Motion of the Center of Mass:
- The net electric force on the system is zero since the forces on the electron and positron cancel each other out. The magnetic forces also cancel out due to equal and opposite forces. Thus, the motion of the center of mass is influenced only by the magnetic field. This statement is also correct.
Conclusion:
The incorrect statement is that "the electric force on both the particles causes identical acceleration."
- An electron enters the cube with velocity v.
- A positron enters the cube with velocity −v.
- The charges are −e for the electron and +e for the positron.
- The electric force on the electron is given by:
Fe=−eE
- The electric force on the positron is given by:
Fp=+eE
- The accelerations can be calculated using F=ma:
- For the electron:
ae=−eEm
- For the positron:
ap=+eEm
- Since ae and ap have opposite signs, they are not identical. Thus, the statement that "the electric force on both the particles causes identical acceleration" is incorrect.
- The magnetic force on the electron is given by:
FBe=−e(v×B)
- The magnetic force on the positron is given by:
FBp=+e(−v×B)=−e(−v×B)=e(v×B)
- The corresponding accelerations are:
- For the electron:
aBe=−e(v×B)m
- For the positron:
aBp=e(v×B)m
- The magnitudes of the magnetic forces are equal, thus the accelerations due to the magnetic force are equal in magnitude but opposite in direction. Therefore, the statement that "the magnetic force on both the particles causes equal acceleration" is correct.
- Both particles have the same charge magnitude and mass. Therefore, they gain or lose energy at the same rate when subjected to the same electric and magnetic fields. This statement is correct.
- The net electric force on the system is zero since the forces on the electron and positron cancel each other out. The magnetic forces also cancel out due to equal and opposite forces. Thus, the motion of the center of mass is influenced only by the magnetic field. This statement is also correct.
The incorrect statement is that "the electric force on both the particles causes identical acceleration."
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS
6 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity →v and a positron enters via opposite face with velocity −→v. At this instant,
View SolutionAn electron enters a region of space in which there exists an electric field 'E' and magnetic field 'B'. If the electron continues to move in the same direction with same velocity as before, the NOT possible case among the following is
View Solution
Knowledge Check
An electron enters with a velocity →v=v0ˆi into a cubical region (faces parallel to coordinate planes) in which there are uniform electric and magnetic fields. The orbit of the electron is found to spiral down inside the cube in plane parallel to the x-y plane. Suggest a configuration of fields →E and →B that can lead to it.
A→E=E0ˆj,→B=B0ˆkB→E=E0ˆi,→B=B0ˆkC→E=E0ˆi,→B=B0ˆjD→E=E0ˆj,→B=B0ˆj
A uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30∘ with x-axis .
Then
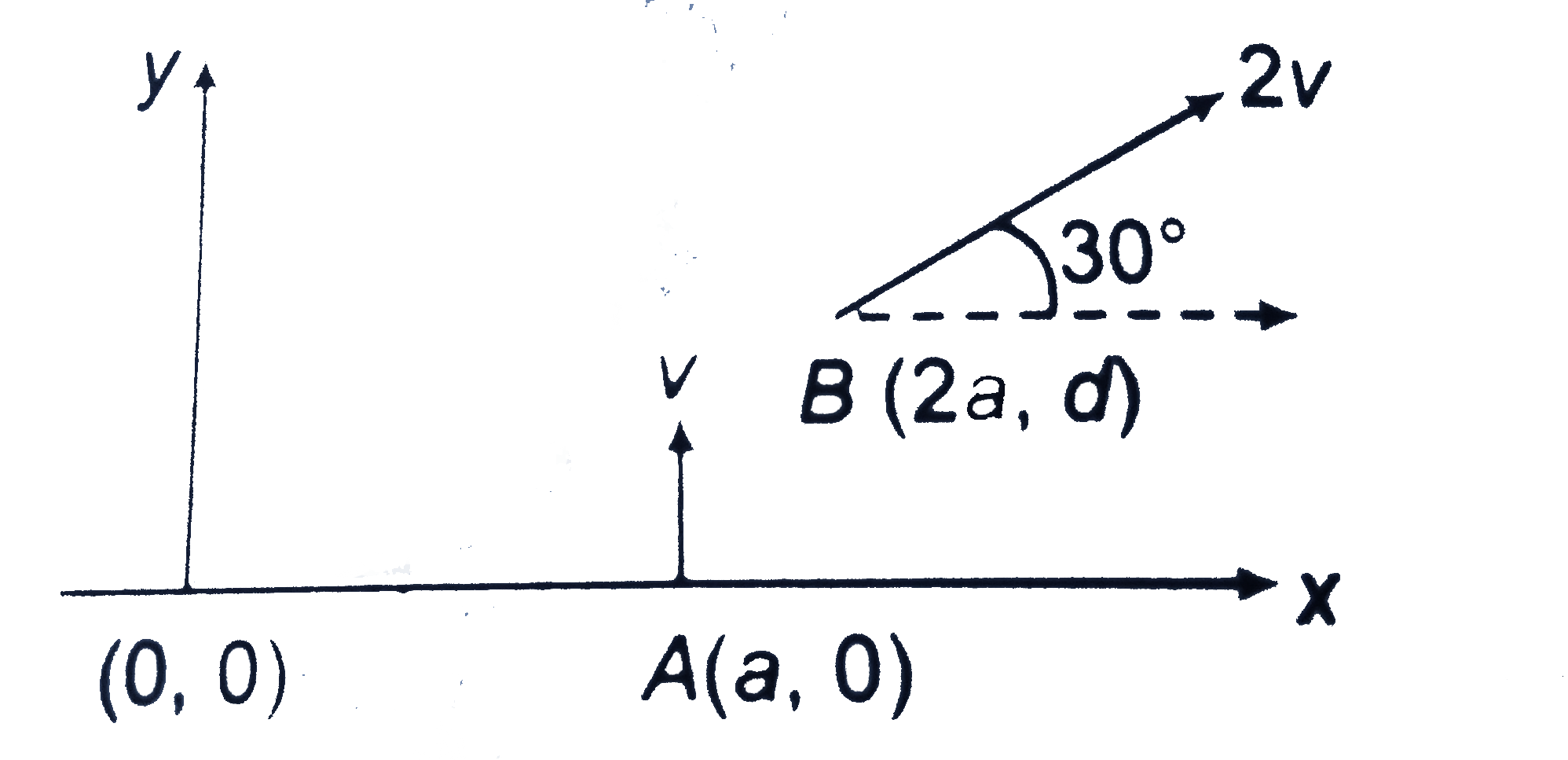
View SolutionA particle of charge -q and mass m enters a uniform magnetic field →B (perpendicular to paper inward) at P with a velocity v0 at an angle α and leaves the field at Q with velocity v at angle β as shown in fig.

View SolutionLet →Eand→B denote the electric and magnetic field in a certain region of space. A proton moving with a velocity along a straight line enters the region and is found to pass through it undeflected. Indicate which of the following statement are consistent with the observation.
View SolutionLet →Eand→B denote the electric and magnetic field in a certain region of space. A proton moving with a velocity along a straight line enters the region and is found to pass through it undeflected. Indicate which of the following statement are consistent with the observation.
View Solutionif E denotes electric field in a uniform conductor and vd the corresponding drift velocity of free electrons in the conductor, then which of the following graph is correct
View SolutionIn a region of space, a uniform magnetic field B exists in the x-direction. An electron is fired from the origin with its initial velocity u making an angle α with the y direction in the y-z plane. In the subsequent motion of the electron,

View SolutionAn electron enters with a velocity →v=v0ˆi into a cubical region (faces parallel to coordinate planes) in which there are uniform electric and magnetic fields. The orbit of the electron is found to spiral down inside the cube in plane parallel to the x-y plane. Suggest a configuration of fields →E and →B that can lead to it.
View Solution
