A charged particle is moving on circular path with velocityv in a uniform magnetic field B, if the velocity of the charged particle is doubled and strength of magnetic field is halved, then radius becomes
8 times
4 times
2 times
16 times
The correct Answer is:B
To solve the problem, we need to understand the relationship between the radius of the circular path of a charged particle moving in a magnetic field and the parameters involved: the velocity of the particle (v), the charge of the particle (q), the magnetic field strength (B), and the radius of the path (r).
1. Understanding the Force on the Charged Particle:
The magnetic force acting on a charged particle moving in a magnetic field is given by:
Fm=qvBsinθ
Since the velocity is perpendicular to the magnetic field, θ=90∘ and sin90∘=1. Therefore, the magnetic force simplifies to:
Fm=qvB
2. Centripetal Force:
The centripetal force required to keep the particle moving in a circular path is given by:
Fc=mv2r
where m is the mass of the particle, v is its velocity, and r is the radius of the circular path.
3. Equating the Forces:
For the particle to move in a circular path, the magnetic force must equal the centripetal force:
qvB=mv2r
4. Solving for Radius:
Rearranging the equation to find the radius r:
r=mvqB
5. Changing Conditions:
According to the problem, the velocity of the charged particle is doubled:
v′=2v
and the strength of the magnetic field is halved:
B′=B2
6. Finding the New Radius:
We can now find the new radius r′ using the new values:
r′=mv′qB′=m(2v)q(B2)
Simplifying this:
r′=2mvqB⋅2=4mvqB
7. Relating New Radius to Original Radius:
From our earlier equation for r:
r=mvqB
Thus, we can express r′ in terms of r:
r′=4⋅mvqB=4r
8. Conclusion:
Therefore, the new radius r′ becomes:
r′=4r
Final Answer:
The radius becomes 4r.
The magnetic force acting on a charged particle moving in a magnetic field is given by:
Fm=qvBsinθ
Since the velocity is perpendicular to the magnetic field, θ=90∘ and sin90∘=1. Therefore, the magnetic force simplifies to:
Fm=qvB
The centripetal force required to keep the particle moving in a circular path is given by:
Fc=mv2r
where m is the mass of the particle, v is its velocity, and r is the radius of the circular path.
For the particle to move in a circular path, the magnetic force must equal the centripetal force:
qvB=mv2r
Rearranging the equation to find the radius r:
r=mvqB
According to the problem, the velocity of the charged particle is doubled:
v′=2v
and the strength of the magnetic field is halved:
B′=B2
We can now find the new radius r′ using the new values:
r′=mv′qB′=m(2v)q(B2)
Simplifying this:
r′=2mvqB⋅2=4mvqB
From our earlier equation for r:
r=mvqB
Thus, we can express r′ in terms of r:
r′=4⋅mvqB=4r
Therefore, the new radius r′ becomes:
r′=4r
The radius becomes 4r.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
A charged particle is moving in a circular path in uniform magnetic field. Match the following.
 View Solution
View SolutionA charged particle moves in a circular path in a uniform magnetic field. If its speed is reduced, then its tiem period will
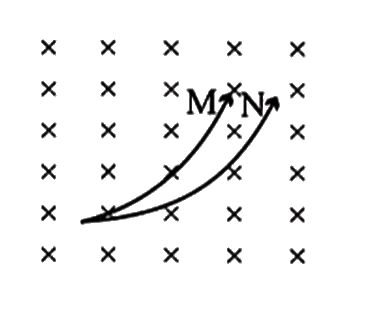
View SolutionTwo charged particle M and N are projected with same velocity in a uniform magnetic field. Then M and N respectively.
 View Solution
View SolutionWhen would a moving charged particle travel undeviated in a uniform magnetic field ?
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionA charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
View SolutionA charged particle is moved along a magnetic field line. The magnetic force on the particle is
View SolutionStatement 1: A charged particle is moving in a circular path under the action of a uniform magnetic field as shown in Fig. During motion kinetic energy of charged particle is costant.
Statement 2: During the motion, magnetic force acting on the particle is perpendicular to instantaneous velocity.
 View Solution
View SolutionA charged particle moves in a uniform magnetic field B=(2ˆi−3ˆj) T
View SolutionIf a charged particle is a plane perpendicular to a uniform magnetic field with a time period T Then
View Solution
