Equipotentials at a great distance from a collection of charges whose total sum is not zero are approximately
spheres
planes
paraboloids
ellipsoids.
The correct Answer is:A
To solve the problem of determining the shape of equipotential surfaces at a great distance from a collection of charges whose total sum is not zero, we can follow these steps:
Step 1: Understand Equipotential Surfaces
Equipotential surfaces are surfaces where the electric potential is the same at every point. For a point charge, these surfaces are spherical in shape.
Hint: Recall that equipotential surfaces are defined by the condition that the electric potential is constant across the surface.
Step 2: Consider a Point Charge
For a single point charge q, the equipotential surfaces are concentric spheres centered around the charge. The potential V at a distance r from the charge is given by the formula:
V=kqr
where k is Coulomb's constant.
Hint: Remember that the potential decreases with distance from the charge, leading to spherical equipotential surfaces.
Step 3: Analyze a Collection of Charges
Now, consider a collection of charges where the total charge Q is not equal to zero. At a great distance from this collection, the behavior of the electric field and potential can be approximated as if it were a single point charge with charge Q.
Hint: Think about how the superposition principle applies to electric fields from multiple charges.
Step 4: Determine the Effective Charge
At a large distance, the entire collection of charges can be treated as a single point charge with the total charge Q. Thus, the potential at a distance r from this collection can be expressed similarly to that of a point charge:
V=kQr
Hint: Consider how the total charge influences the potential at large distances.
Step 5: Conclude the Shape of Equipotential Surfaces
Since the potential behaves like that of a point charge at a large distance, the equipotential surfaces for this collection of charges will also be spherical. Therefore, at a great distance from the collection of charges, the equipotential surfaces are approximately spherical.
Hint: Relate the concept of distance and charge distribution to the resulting shape of the equipotential surfaces.
Final Answer
The equipotential surfaces at a great distance from a collection of charges whose total sum is not zero are approximately spheres.
Equipotential surfaces are surfaces where the electric potential is the same at every point. For a point charge, these surfaces are spherical in shape.
For a single point charge q, the equipotential surfaces are concentric spheres centered around the charge. The potential V at a distance r from the charge is given by the formula:
V=kqr
where k is Coulomb's constant.
Now, consider a collection of charges where the total charge Q is not equal to zero. At a great distance from this collection, the behavior of the electric field and potential can be approximated as if it were a single point charge with charge Q.
At a large distance, the entire collection of charges can be treated as a single point charge with the total charge Q. Thus, the potential at a distance r from this collection can be expressed similarly to that of a point charge:
V=kQr
Since the potential behaves like that of a point charge at a large distance, the equipotential surfaces for this collection of charges will also be spherical. Therefore, at a great distance from the collection of charges, the equipotential surfaces are approximately spherical.
The equipotential surfaces at a great distance from a collection of charges whose total sum is not zero are approximately spheres.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTPS ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSERTION & REASON
Explore 15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTPS ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Electric Potential
Explore 3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTPS ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:HOTS
Explore 5 Videos
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTPS ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Assertion And Reason
Explore 15 Videos
- MAGNETISM AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:MAGNETISM AND MATTER Exercise:NCERT Exemplar
Explore 5 Videos
Similar Questions
Knowledge Check
The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential ϕ at that point is
AWQxBWCWxDWQ
A solid sphere of radius R has total charge 2Q and volume charge density p=kr where r is distance from centre. Now charges Q and −Q are placed diametrically opposite at distance 2a where a is distance form centre of sphere such that net force on charge Q is zero then relation between a and R is
View SolutionA particle of mass m carrying charge q is projected with velocity v from point P toward aninfinite line of charge from a distance a . Its speed reduces to zero momentarily at point Q, which is at a distance a/2 from the line of charge. If another particle with mass m and charge −q is projected with the same velosity v from P toward the line of charge, what will be its speed at Q ?
View SolutionThe magnitude of electric intensity at a distance x from a charge q is E.An identical charge is placed at a distance 2x from it Then the magnitude of the force it experience is ..
View SolutionEquipotential spheres are drawn round a point charge. As we move away from charge will the spacing between two spheres having a constant potential difference decrease, increase or remain constant.
View SolutionEquipotential spheres are drawn round a point charge. As we move away from charge will the spacing between two spheres having a constant potential difference decrease, increase or remain constant.
View SolutionCharges Q and -2Q are placed at some distance. The locus of points in the plane of the charges where the potential is zero will be :
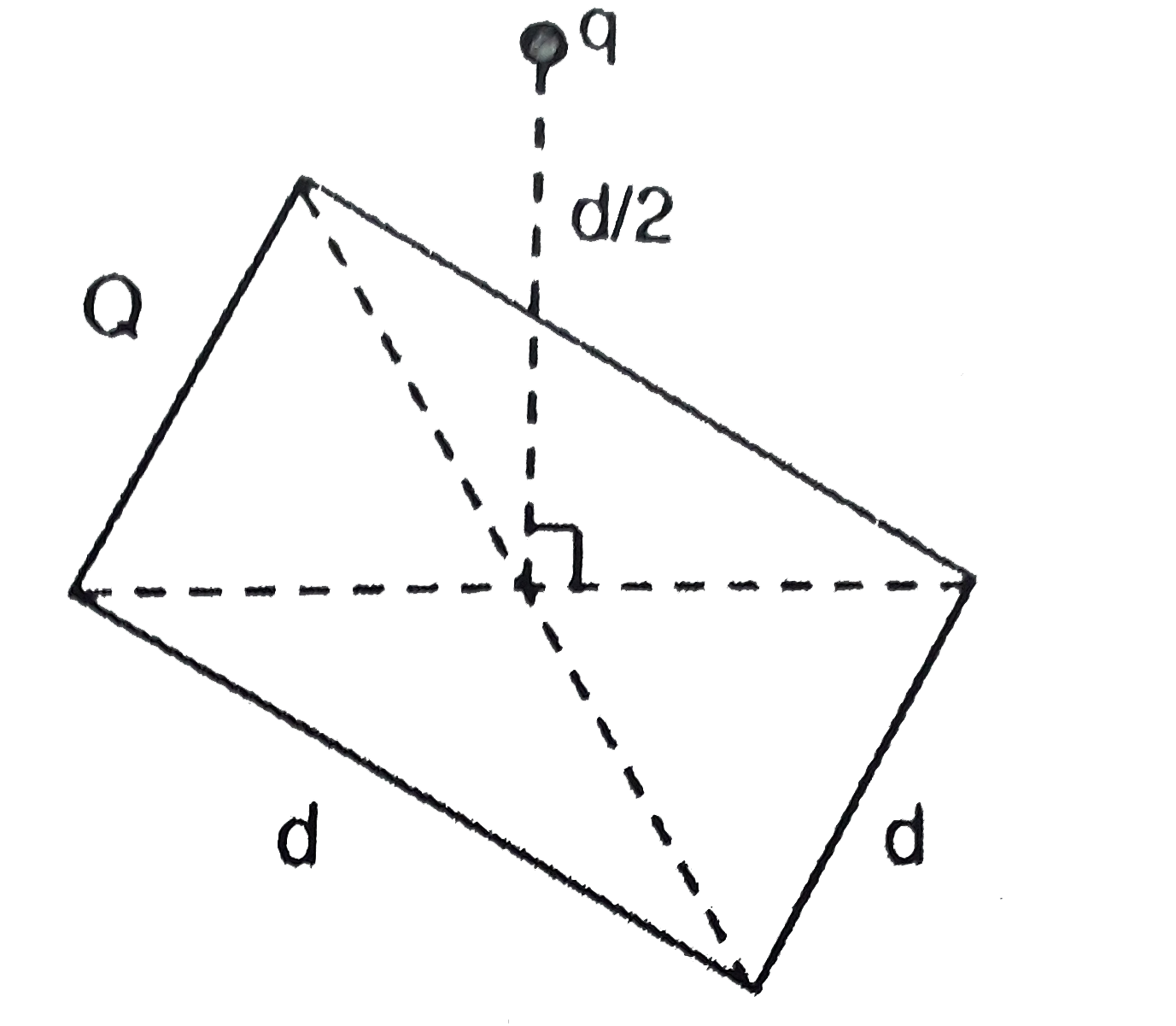
View SolutionA square of side d, made from a thin insulating plate, is uniformly charged and carries a total charge of Q. A point charge q is placed on the symmetrical normal axis of the square at a distance d/2 from the plate. How large is the force acting on the point charge ?
View Solution

