A parallel plate capacitor has a uniform electric field E in the space between the the plates. If the distance between the plates is d and area of each plate is A, the energy stored in the capacitor is
12ε0E2
E2Adε0
12ε0E2Ad
eisi0E2Ad
The correct Answer is:C
To find the energy stored in a parallel plate capacitor given the uniform electric field E, distance between the plates d, and area of each plate A, we can follow these steps:
Step 1: Understand the relationship between capacitance, voltage, and energy
The energy U stored in a capacitor can be expressed as:
U=12CV2
where C is the capacitance and V is the voltage across the capacitor.
Step 2: Determine the capacitance of a parallel plate capacitor
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0Ad
where ε0 is the permittivity of free space, A is the area of the plates, and d is the distance between the plates.
Step 3: Relate the electric field to voltage
The electric field E between the plates is related to the voltage V and the distance d by the equation:
E=Vd
From this, we can express the voltage V as:
V=E⋅d
Step 4: Substitute the expressions for capacitance and voltage into the energy formula
Now, substituting C and V into the energy formula:
U=12(ε0Ad)(E⋅d)2
Step 5: Simplify the expression
Substituting V into the energy equation gives:
U=12(ε0Ad)(E2d2)
This simplifies to:
U=12ε0AE2d
Step 6: Final expression for energy stored in the capacitor
Thus, the energy stored in the parallel plate capacitor is:
U=12ε0AE2d
Final Result
The energy stored in the capacitor is:
U=12ε0AE2d
---
The energy U stored in a capacitor can be expressed as:
U=12CV2
where C is the capacitance and V is the voltage across the capacitor.
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0Ad
where ε0 is the permittivity of free space, A is the area of the plates, and d is the distance between the plates.
The electric field E between the plates is related to the voltage V and the distance d by the equation:
E=Vd
From this, we can express the voltage V as:
V=E⋅d
Now, substituting C and V into the energy formula:
U=12(ε0Ad)(E⋅d)2
Substituting V into the energy equation gives:
U=12(ε0Ad)(E2d2)
This simplifies to:
U=12ε0AE2d
Thus, the energy stored in the parallel plate capacitor is:
U=12ε0AE2d
The energy stored in the capacitor is:
U=12ε0AE2d
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
A parallel plate condenser has a unifrom electric field E(V/m) in the space between the plates. If the distance between the plates is d(m) and area of each plate is A(m2) the energy (joule) stored in the condenser is
View SolutionA parallel plate condenser has a unifrom electric field E(V/m) in the space between the plates. If the distance between the plates is d(m) and area of each plate is A(m2) the energy (joule) stored in the condenser is
View Solution
Knowledge Check
As the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.A parallel plate capacitor with air between the plates has a capacitance of 10 pF. The capacitance, if the distance bgetween the plates is reduced by half and the space between tehm is filled with a substance of dielectric constant 4 is
A80pFB96pFC100pFD120pF
A parallel plate capacitor has an electric field of 105V/m between the plates. If the charge on the capacitor plate is 1μC, then force on each capacitor plate is-
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionIn a parallel plate capacitor, the distance between the plates is d and potential difference across the plate is V. Energy stored per unit volume between the plates of capacitor is
View SolutionTo reduce the capacitance of parallel plate capacitor, the space between the plate is
View SolutionIf the separation between the plates of a capacitor is 5 mm , then area of the plate of a 3 F parallel plate capacitor is
View SolutionAnswer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
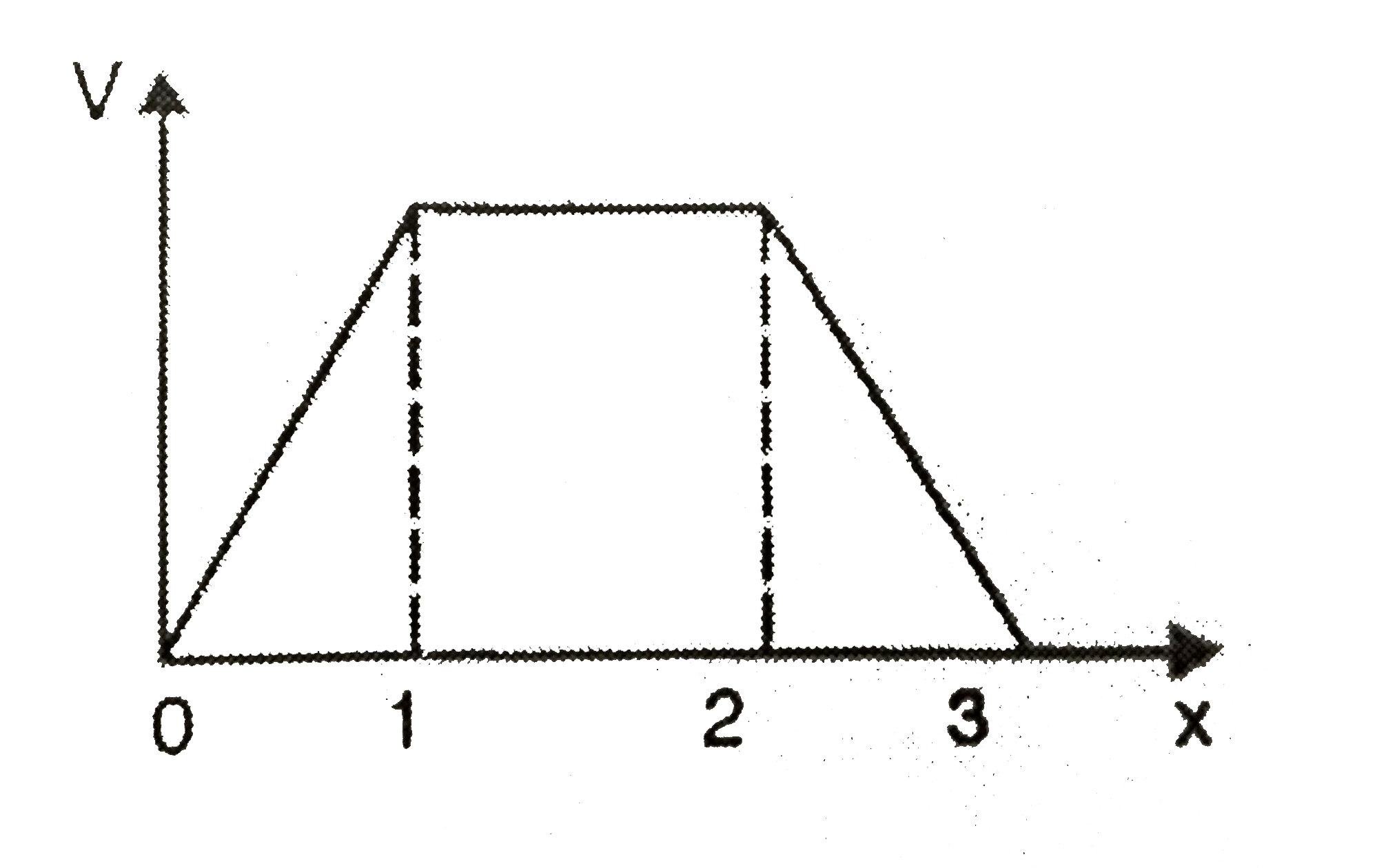
View Solution
