A capacitor is made of two circular plates of radius R each, separated by a distance d<<R. The capacitor is connected to a constant voltage. A thin conducting disc of radius r<<R and thickness t<<r is placed at a center of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m.
√mgdπε0r2
√mgdπε0r
√mgd2πε0r2
√mgdπε0r2
The correct Answer is:C
To find the minimum voltage required to lift the thin conducting disc placed at the center of the bottom plate of a capacitor, we can follow these steps:
Step 1: Understand the System
We have a capacitor made of two circular plates with radius R and separated by a distance d (where d≪R). A thin conducting disc of radius r (where r≪R) and thickness t (where t≪r) is placed at the center of the bottom plate.
Step 2: Electric Field in the Capacitor
The electric field E between the plates of the capacitor is given by:
E=Vd
where V is the voltage across the plates.
Step 3: Charge on the Disc
The charge Q′ on the disc can be calculated using the capacitance C of the capacitor. The capacitance of a parallel plate capacitor is given by:
C=ϵ0Ad
where A is the area of the plates. For our circular plates, the area A is:
A=πR2
Thus, the capacitance becomes:
C=ϵ0πR2d
The charge Q′ on the capacitor is:
Q′=C⋅V=ϵ0πR2d⋅V
Step 4: Force on the Disc
The force F acting on the disc due to the electric field is given by:
F=Q′⋅E
Substituting the expressions for Q′ and E:
F=(ϵ0πR2d⋅V)⋅(Vd)=ϵ0πR2V2d2
Step 5: Condition for Lifting the Disc
For the disc to lift off, the force F must be equal to or greater than the weight of the disc mg:
ϵ0πR2V2d2=mg
Step 6: Solve for Voltage V
Rearranging the equation to solve for V:
V2=mgd2ϵ0πR2
Taking the square root gives:
V=√mgd2ϵ0πR2
Final Expression for Minimum Voltage
Thus, the minimum voltage required to lift the disc is:
V=√mgd2ϵ0πr2
We have a capacitor made of two circular plates with radius R and separated by a distance d (where d≪R). A thin conducting disc of radius r (where r≪R) and thickness t (where t≪r) is placed at the center of the bottom plate.
The electric field E between the plates of the capacitor is given by:
E=Vd
where V is the voltage across the plates.
The charge Q′ on the disc can be calculated using the capacitance C of the capacitor. The capacitance of a parallel plate capacitor is given by:
C=ϵ0Ad
where A is the area of the plates. For our circular plates, the area A is:
A=πR2
Thus, the capacitance becomes:
C=ϵ0πR2d
The charge Q′ on the capacitor is:
Q′=C⋅V=ϵ0πR2d⋅V
The force F acting on the disc due to the electric field is given by:
F=Q′⋅E
Substituting the expressions for Q′ and E:
F=(ϵ0πR2d⋅V)⋅(Vd)=ϵ0πR2V2d2
For the disc to lift off, the force F must be equal to or greater than the weight of the disc mg:
ϵ0πR2V2d2=mg
Rearranging the equation to solve for V:
V2=mgd2ϵ0πR2
Taking the square root gives:
V=√mgd2ϵ0πR2
Thus, the minimum voltage required to lift the disc is:
V=√mgd2ϵ0πr2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTPS ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:HOTS
Explore 5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTPS ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:EXEMPLAR PROBLEMS
Explore 3 Videos
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTPS ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Assertion And Reason
Explore 15 Videos
- MAGNETISM AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:MAGNETISM AND MATTER Exercise:NCERT Exemplar
Explore 5 Videos
Similar Questions
The two metallic plates of radius r are placed at a distance d apart and its capacity is C. If a plate of radius r/2 and thickness dof dielectric constant 6 is placed between the plates of the condenser, then its capacity will be
View SolutionA parallel plate capacitor consists of two circular plates of radius R=0.1 m. they are separated by a distance d=0.5mm, if electric field between the capacitor plates changes as dEdt=5×1013Vm×s. Find displacement current between the plates.
View Solution
Knowledge Check
A capacitor made of two circular plates each of radius 12 cm and separated by 5 cm. The capacitor is being charged by an external source. The charging current is constant and equal to 0.15 A. The capacitance of the parallel plate capacitor is
 A40 pFB45 pFC70 pFD80 pF
A40 pFB45 pFC70 pFD80 pF
A disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionA parallel plate capacitor consists of two circular plate of radius R=0.1m. They are separated by a short distance. If electric field between the capacitor plates changes as dEdt=6×1013Vm×s. Find displacement current between the plates.
View SolutionFigure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.

View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View Solution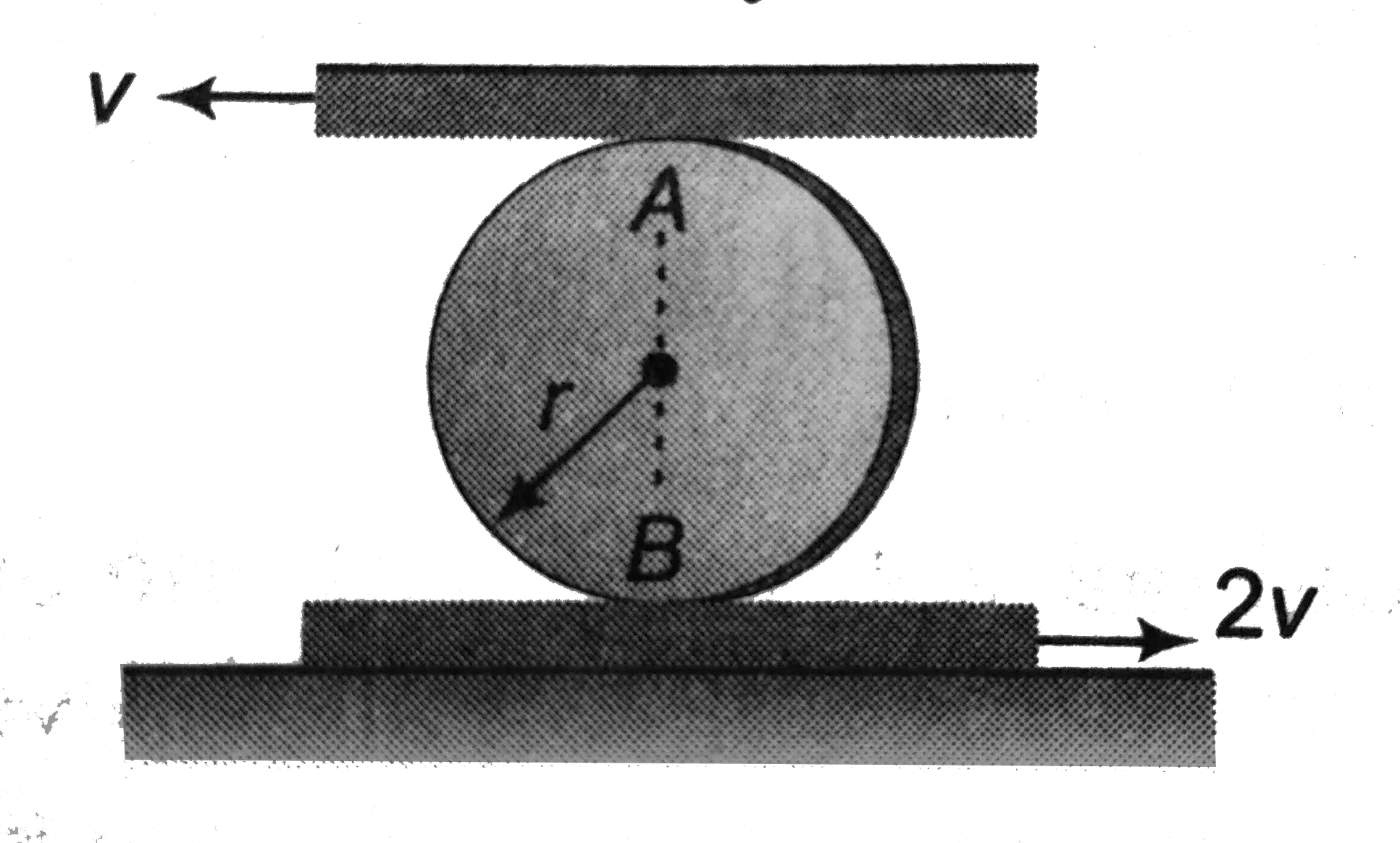
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View SolutionA point charge q is placed at a point on the axis of a non-conducting circular plate of radius r at a distance R(>>r) from its center. The electric flux associated with the plate is
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View Solution

