A slab of material of dielectric constant K has the same area as the plates of a parallel capacitor, but has a thickness (34d),
where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates
C=ε0Ad(K+34K)
C=ε0Ad(2KK+3)
C=ε0Ad(KK+3)
C=ε0Ad(4KK+3)
The correct Answer is:D
To solve the problem of how the capacitance changes when a dielectric slab is inserted between the plates of a parallel plate capacitor, we can follow these steps:
Step 1: Understand the Capacitance Formula
The capacitance C of a parallel plate capacitor without any dielectric is given by the formula:
C0=Aϵ0d
where:
- A is the area of the plates,
- ϵ0 is the permittivity of free space,
- d is the separation between the plates.
Step 2: Insert the Dielectric Slab
When a dielectric slab of thickness t=34d and dielectric constant K is inserted between the plates, the effective capacitance can be calculated using the modified formula:
C=Aϵ0d−t+Aϵ0t/K
This formula accounts for the two regions: one with the dielectric and one without.
Step 3: Substitute the Values
Substituting t=34d into the formula:
C=Aϵ0d−34d+Aϵ034d/K
This simplifies to:
C=Aϵ014d+Aϵ0K34d
Step 4: Simplify Each Term
Calculating each term:
1. The first term becomes:
C1=Aϵ014d=4Aϵ0d
2. The second term becomes:
C2=Aϵ0K34d=4Aϵ0K3d
Step 5: Combine the Terms
Now, we can combine C1 and C2:
C=4Aϵ0d+4Aϵ0K3d
Factoring out 4Aϵ0d:
C=4Aϵ0d(1+K3)
Step 6: Final Expression
Thus, the final expression for the capacitance when the slab is inserted is:
C=4Aϵ0d(3+K3)
Conclusion
The capacitance increases when the dielectric slab is inserted, and the final capacitance can be expressed as:
C=4Aϵ0(3+K)3d
The capacitance C of a parallel plate capacitor without any dielectric is given by the formula:
C0=Aϵ0d
where:
- A is the area of the plates,
- ϵ0 is the permittivity of free space,
- d is the separation between the plates.
When a dielectric slab of thickness t=34d and dielectric constant K is inserted between the plates, the effective capacitance can be calculated using the modified formula:
C=Aϵ0d−t+Aϵ0t/K
This formula accounts for the two regions: one with the dielectric and one without.
Substituting t=34d into the formula:
C=Aϵ0d−34d+Aϵ034d/K
This simplifies to:
C=Aϵ014d+Aϵ0K34d
Calculating each term:
1. The first term becomes:
C1=Aϵ014d=4Aϵ0d
2. The second term becomes:
C2=Aϵ0K34d=4Aϵ0K3d
Now, we can combine C1 and C2:
C=4Aϵ0d+4Aϵ0K3d
Factoring out 4Aϵ0d:
C=4Aϵ0d(1+K3)
Thus, the final expression for the capacitance when the slab is inserted is:
C=4Aϵ0d(3+K3)
The capacitance increases when the dielectric slab is inserted, and the final capacitance can be expressed as:
C=4Aϵ0(3+K)3d
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
A slab of materail of dielectric constant K has the same area as the plates of a parallel plate capacitor but has thickness d/2, where d is the separation between the plates. Find the expression for the capacitance when the slab is inserted between the plates.
View SolutionA parallel plate capacitor of plate area A and plate separation d is charged to potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. If Q, E and W denote respectively, the magnitude of charge on each plate, the electric field between the plates (after the slab is inserted), and work done on the system, in question, in the process of inserting the slab, then
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View SolutionA parallel plate capacitor consists of two metal plates of area A and separation d. A slab of thickness t and electric constant K is inserted between the plates with its faces parallel to the plates and having the same surface area as that of the plates. Find the capacitance of the system.
IF K=2, for what value of t/d will the capacitance of the system be 3/2 times that of the air capacitor? Calculate the energy in the two cases and account for the energy change.
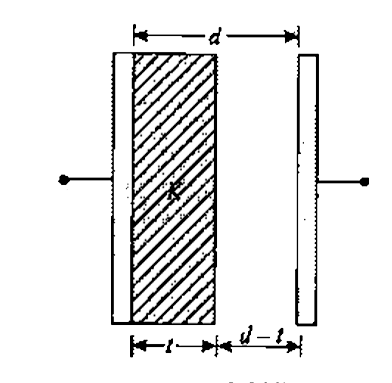
View SolutionA slab of copper of thickness y is inserted between the plates of parallel plate capacitor as shown in figure. The separation between the plates is d. If y=d4, then the ratio of capacitance of the capacitor after nd before inserting the slab is

View SolutionA slab of copper of thickness b is inserted in between the plates of parallel plate capacitor as shown in figure. The separation of the plate is d. If b=d/2, then the ratio of capacities of the capacitor after and before inserting that slab will be

View SolutionA dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionSeparation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
View SolutionA dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
A. become zero
B. remains the same
C. decrease
D. increase
View Solution
