If the dielectric constant and dielectirc strength be denoted by K and x respectively, then a meterial suitable for use as a dielectric in a capacitor must have
high K and high X
high K and low K
low K and high K
low K and low X
The correct Answer is:A
The material suitable for using as a dielectric must have high dielectric strenght X and large dielectric constant K.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
Which of the following set of characteristics of a material is suitable for using it as a dielectric in a capacitor?
View SolutionA parallel plate capacitor is to be designed with a voltage rating 1 KV using a material of dielectric constant 3 and dielectric strength about 107Vm−1. [Dielectric strength is the maximum electric field a material can tolerate without break down, i.e, without starting to conduct electrically through partial ionization. For safety, we should like the field never to exceed say 10% of the dielectric strength]. What minimum area of the plates is required to have a capacitance of 50 pF ?
View Solution
Knowledge Check
For metals the value of dielectric constant (K) is
AzeroBinfiniteC1D10
A parallel plate capacitor is formed by two plates, each of area 100cm2, separated by a distance of 1 mm. A dielectric of dielectric constant 5.0 and dielectric strength 1.9X107Vm−1 is filled between the plates. Find the maximum charge that can be stored on the capacitor without causing any dielectric breakdown.
View SolutionA parallel plate capacitor is to be designed which is to be connected across 1kv potential.The dielectric meteral which is to be Filled between the plates has dielectric constant K=6π and dielectric strenght 107V/m.For safly the eletric field is never to exceed 10 % of the dielectirc strenght.With such specification, of we want a capacitor of 50pF, What minumim area (in mm2) of plates is required for safe working ?
(use ε0=136π×10−9inMKS)
View SolutionThe dielectric to be used in a parallel-plate capacitor has a dielectric constant of 3.60 and a dielectric strength of 1.60×107V/m. The capacitor is to have a capacitance of 1.25×10−9F and must be able to withstand a maximum potential difference of 5500V. What is the minimum area the plates of the capacitor may have?
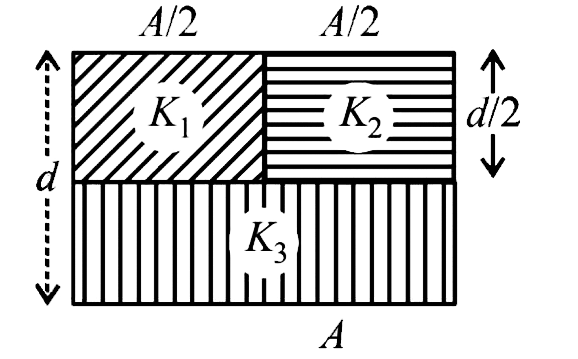
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1, k2 and k3 as shown. If a isngle dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectic constant k is given by
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials hving dielectric constants K1,K2,K3 and K4 as shown in the figure below. If a single dielectric material is to be used to have the same capacitance c in this capacitor, then its dielectric constant K is given by

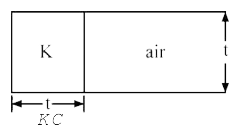
View SolutionA parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
View SolutionAssertion : When a dielectric is placed in an electric field, the electric field with in the dielectric as well as. Potential difference across the capacitor plates are reduced by a factor K (battery is not connected).
Reason : The dielectric constant is the ratio of the absolute permittivity of the dielectric to the to the permittivity of the free space.
View Solution
