The electrostatic attracting froce on a small sphere of charge 0.2μC due to another small sphere of charge −0.4μC in air is 0.4N. The distance between the two spheres is
43.2×10−6m
42.4×10−3m
18.1×10−3m
19.2×10−6m
The correct Answer is:B
To find the distance between the two spheres, we can use Coulomb's law, which states that the electrostatic force F between two point charges q1 and q2 is given by the formula:
F=k|q1q2|r2
where:
- F is the electrostatic force,
- k is Coulomb's constant (8.99×109N m2/C2),
- q1 and q2 are the charges,
- r is the distance between the charges.
1. Identify the Given Values:
- Charge q1=0.2μC=0.2×10−6C
- Charge q2=−0.4μC=−0.4×10−6C
- Electrostatic force F=0.4N
2. Convert Charges to Standard Units:
- q1=0.2×10−6C=2×10−7C
- q2=−0.4×10−6C=−4×10−7C
3. Substitute Values into Coulomb's Law:
0.4=k|(2×10−7)(−4×10−7)|r2
Since we are interested in the magnitude of the force, we can ignore the negative sign.
4. Insert the Value of k:
0.4=(8.99×109)(2×10−7)(4×10−7)r2
5. Calculate the Product of Charges:
|(2×10−7)(4×10−7)|=8×10−14
6. Rearranging the Equation to Solve for r2:
0.4=(8.99×109)8×10−14r2
r2=(8.99×109)8×10−140.4
7. Calculating the Right Side:
r2=(8.99×109)×(2×10−13)=1.798×10−3
8. Taking the Square Root to Find r:
r=√1.798×10−3≈0.0424m
9. Convert to Millimeters:
r≈42.4mm
Final Answer:
The distance between the two spheres is approximately 0.0424m or 42.4mm.
- F is the electrostatic force,
- k is Coulomb's constant (8.99×109N m2/C2),
- q1 and q2 are the charges,
- r is the distance between the charges.
- Charge q1=0.2μC=0.2×10−6C
- Charge q2=−0.4μC=−0.4×10−6C
- Electrostatic force F=0.4N
- q1=0.2×10−6C=2×10−7C
- q2=−0.4×10−6C=−4×10−7C
0.4=k|(2×10−7)(−4×10−7)|r2
Since we are interested in the magnitude of the force, we can ignore the negative sign.
0.4=(8.99×109)(2×10−7)(4×10−7)r2
|(2×10−7)(4×10−7)|=8×10−14
0.4=(8.99×109)8×10−14r2
r2=(8.99×109)8×10−140.4
r2=(8.99×109)×(2×10−13)=1.798×10−3
r=√1.798×10−3≈0.0424m
r≈42.4mm
The distance between the two spheres is approximately 0.0424m or 42.4mm.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:NCERT FINGERTPS ENGLISHChapter:ELECTRIC CHARGES AND FIELDSExercise:ASSERTION & REASON
Explore 15 Videos
- ELECTRIC CHARGES AND FIELDSBook:NCERT FINGERTPS ENGLISHChapter:ELECTRIC CHARGES AND FIELDSExercise:Electric Charges
Explore 5 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTPS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:NCERT Exemplar
Explore 6 Videos
Similar Questions
The electrostatic force on a small sphere of charge 0.4μC due to another small sphere of charge −0.8μC in air 0.2 N (i) What is the distance between the two spheres? (ii) What is the force on the second sphere due to the first ?
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png)
View Solution
Knowledge Check
The electrostatic potential energy of two point charges, 1μC each, placed 1 metre apart in air is :
A9×103JB9×109JC9×10−3JD9×10−3J
The force of attractions between two charges 8μC and −4μC is 0.2 N. Find the distance of separation.
View SolutionA hollow sphere of radius 2R is charged to V volts and another smaller sphere of radius R is charged to V/2 volts. Now the smaller sphere is placed inside the bigger sphere without changing the net charge on each sphere. The potential difference between the two spheres would be
View SolutionA sherical capacitor has an inner sphere of radius 12cm and an outer spere of radius 13cm. The outer sphere is earthed, and the inner sphere is given a charge of 2.5μC. The space between the concentric spjheres is filled with a liquid of dielectric caonstant 32. Determine the potential of the inner sphere.
View SolutionA hollow sphere of radius 2R is charged to V volts and another smaller sphere of radius R is charged to V/2 volts. Then the smaller sphere is placed inside the bigger sphere without changing the net charge on each sphere. The potential difference between the two spheres would becomes V/n. find value of n
View SolutionThe force of repulsion between two point charges is F, when these are at distance 0.5m apart. Now the point charges are replaced by spheres of radii 5 cm each having the same charge as that of the respective point charge. The distance between their centres is again kept 0.5 m. Then the force of repulsion will
View SolutionIn two cases, two identical conducting sphere are given equal charges, in one case of the same type whereas in another case of opposite type. The distance between the spheres is not large comparing with the diameter. Let F1 and F2 be the magnitudes of the force of interaction between the spheres, as shown, then
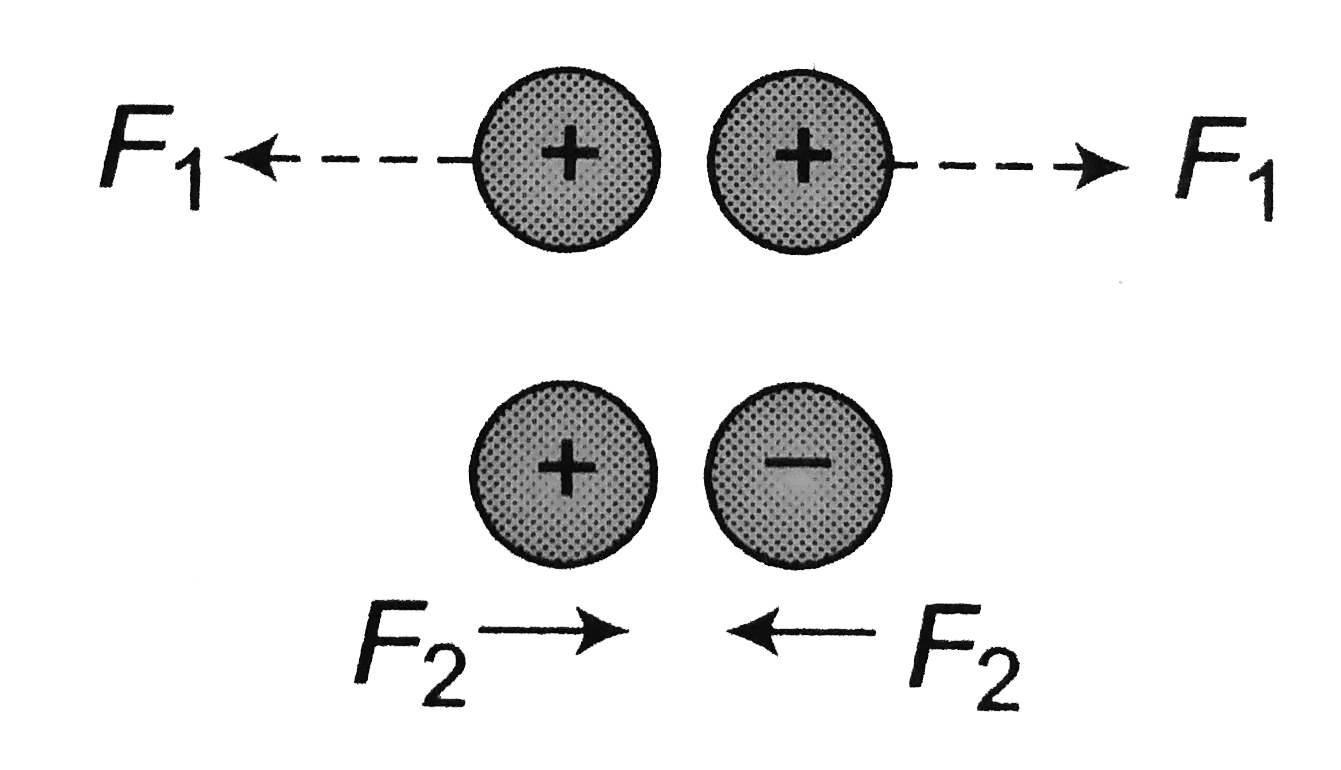
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
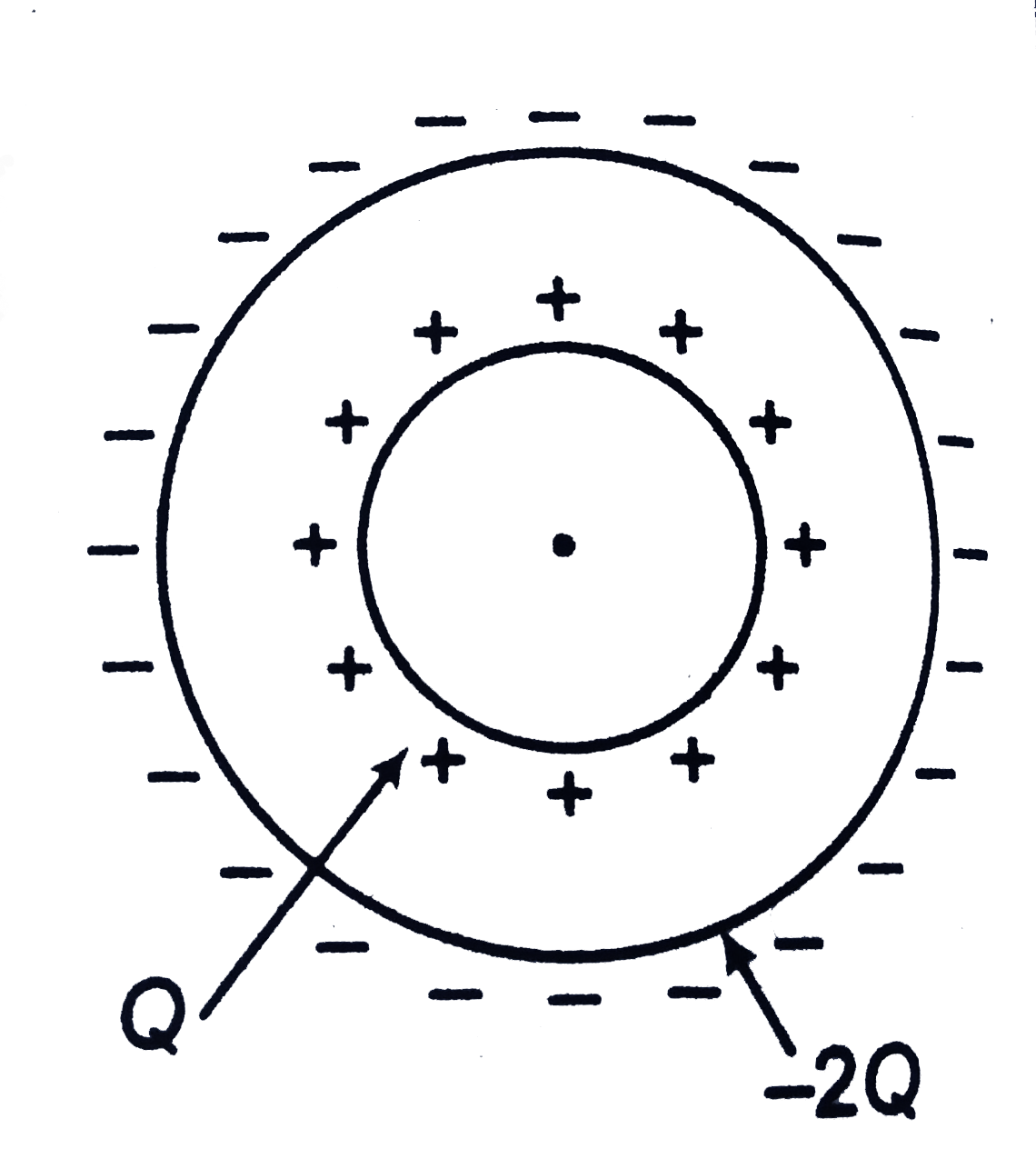
View Solution