What will be the input of A and B for the Boolean expression ¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B).¯¯¯¯¯¯¯¯¯¯¯(A.B)=1?
(0,0)
(0,1)
(1,0)
(1,1)
The correct Answer is:A
To solve the Boolean expression ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)⋅¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=1, we will follow these steps:
Step 1: Rewrite the Expression
We start with the given expression:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)⋅¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=1
This means that both ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B) and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B) must be true (equal to 1) for the entire expression to equal 1.
Step 2: Analyze ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)
The expression ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B) is true when both A and B are false (0). This is because:
- If A=0 and B=0, then A+B=0 and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)=1.
- If either A or B is 1, then A+B=1 and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)=0.
Step 3: Analyze ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)
The expression ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B) is true when at least one of A or B is false (0). This is because:
- If A=0 or B=0, then A⋅B=0 and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=1.
- If both A and B are 1, then A⋅B=1 and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=0.
Step 4: Combine the Conditions
For the entire expression to be true (=1), both conditions must hold:
1. ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)=1 implies A=0 and B=0.
2. ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=1 is satisfied if at least one of A or B is 0.
Since the first condition requires both A and B to be 0, this will also satisfy the second condition.
Conclusion
Thus, the only inputs for A and B that satisfy the Boolean expression ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)⋅¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=1 are:
A=0,B=0
We start with the given expression:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)⋅¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=1
This means that both ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B) and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B) must be true (equal to 1) for the entire expression to equal 1.
The expression ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B) is true when both A and B are false (0). This is because:
- If A=0 and B=0, then A+B=0 and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)=1.
- If either A or B is 1, then A+B=1 and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)=0.
The expression ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B) is true when at least one of A or B is false (0). This is because:
- If A=0 or B=0, then A⋅B=0 and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=1.
- If both A and B are 1, then A⋅B=1 and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=0.
For the entire expression to be true (=1), both conditions must hold:
1. ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)=1 implies A=0 and B=0.
2. ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=1 is satisfied if at least one of A or B is 0.
Thus, the only inputs for A and B that satisfy the Boolean expression ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)⋅¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A⋅B)=1 are:
A=0,B=0
Topper's Solved these Questions
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - HOTS
8 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - NCERT
8 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT Exemplar
11 Videos
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
What does the last stanza of the poem, 'Crossing the Bar'.express?
Adeath has to be awaitedBdeath is painfulCdeath is a fearful plungeDdeath has to be serenely acceptedPoint A, B, and C all lie on a line. Point D is midpoint of ¯¯¯¯¯¯AB and E is the midpoint of BC,¯¯¯¯¯¯AB=4and¯¯¯¯¯¯BC=10. Which of the following could be the length of ¯¯¯¯¯¯AE?
A1B2C3D4
An AND gate is following by a NOT gate in series. With two inputs A & B, the Boolean expression for the out put Y will be :
View SolutionThe diagram shows a coil wound around a U shape soft iron bar AB.
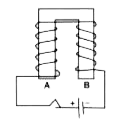
What will be the polarities at A and B if the direction of current is reversed in the circuit ?
View SolutionIf A = 1 and B = 0, then in terms of Boolean algebra , A+¯¯¯B= .
View SolutionName the gate , which represents the Boolean expression y = A. B for inputs A, B
View SolutionIf A, B, C, be the centres of three co-axial circles and t1,t2,t3 be the lengths of the tangents of them any piont, prove that
¯¯¯¯¯¯BC.t21+¯¯¯¯¯¯CA.t22+¯¯¯¯¯¯AB.t23=0
View SolutionIf A,B and C are the elements of Boolean algebra, simplify the expression (A'+B') (A+C')+B' (B+C). Draw the simplified circuit.
View Solution
