An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
eh4πm
eh2πm
eh24πm
e2h4πm
The correct Answer is:A
To find the orbital magnetic dipole moment of an electron in the ground state of a hydrogen atom, we can follow these steps:
Step 1: Understand the Formula for Magnetic Dipole Moment
The orbital magnetic dipole moment (μ) is given by the formula:
μ=i⋅A
where i is the current and A is the area of the circular orbit.
Step 2: Calculate the Area of the Orbit
The area A of a circular orbit with radius R is:
A=πR2
Step 3: Determine the Current i
The current i due to the revolving electron can be calculated using the charge of the electron (e) and the time period (T) of the revolution:
i=eT
The time period T is given by:
T=2πRv
where v is the velocity of the electron.
Step 4: Find the Velocity of the Electron
For an electron in a circular orbit, we can use the quantization of angular momentum:
mvR=nh2π
For the ground state of hydrogen, n=1:
mvR=h2π
From this, we can express the velocity v:
v=h2πmR
Step 5: Substitute Velocity into Time Period
Now substituting v into the expression for T:
T=2πRh2πmR=4π2mR2h
Step 6: Substitute Time Period into Current
Now substituting T back into the expression for current i:
i=eT=eh4π2mR2
Step 7: Substitute Current and Area into Magnetic Dipole Moment
Now substituting i and A into the magnetic dipole moment formula:
μ=i⋅A=(eh4π2mR2)⋅(πR2)
This simplifies to:
μ=eh4πm
Final Answer
Thus, the orbital magnetic dipole moment of the electron in the ground state of the hydrogen atom is:
μ=eh4πm
The orbital magnetic dipole moment (μ) is given by the formula:
μ=i⋅A
where i is the current and A is the area of the circular orbit.
The area A of a circular orbit with radius R is:
A=πR2
The current i due to the revolving electron can be calculated using the charge of the electron (e) and the time period (T) of the revolution:
i=eT
The time period T is given by:
T=2πRv
where v is the velocity of the electron.
For an electron in a circular orbit, we can use the quantization of angular momentum:
mvR=nh2π
For the ground state of hydrogen, n=1:
mvR=h2π
From this, we can express the velocity v:
v=h2πmR
Now substituting v into the expression for T:
T=2πRh2πmR=4π2mR2h
Now substituting T back into the expression for current i:
i=eT=eh4π2mR2
Now substituting i and A into the magnetic dipole moment formula:
μ=i⋅A=(eh4π2mR2)⋅(πR2)
This simplifies to:
μ=eh4πm
Thus, the orbital magnetic dipole moment of the electron in the ground state of the hydrogen atom is:
μ=eh4πm
Topper's Solved these Questions
- ATOMS Book:NCERT FINGERTPS ENGLISHChapter:ATOMS Exercise:Higher order thinking skills
Explore 8 Videos
- ATOMS Book:NCERT FINGERTPS ENGLISHChapter:ATOMS Exercise:NCERT Examplar problems
Explore 7 Videos
- ALTERNATING CURRENT Book:NCERT FINGERTPS ENGLISHChapter:ALTERNATING CURRENT Exercise:Assertion And Reason
Explore 15 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTPS ENGLISHChapter:COMMUNITCATION SYSTEMSExercise:Assertion And Reason
Explore 30 Videos
Similar Questions
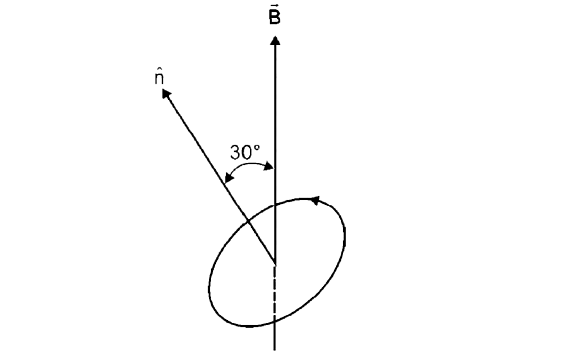
An electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.
View SolutionThe minimum magnetic dipole moment of electron in hydrogen atom is
View SolutionMagnetic moment of an electron in nth orbit of hydrogen atom is
View SolutionMagnetic moment of an electron in nth orbit of hydrogen atom is
View SolutionWhen an electron revolving in the ground state of a hydrogen atom jumps to its 2nd excited state.
View SolutionThe angular speed of electron in the nth orbit of hydrogen atom is
View SolutionThe acceleration of electron in the first orbits of hydrogen atom is
View SolutionThe acceleration of electron in the first orbits of hydrogen atom is
View SolutionWhen an electron in hydrogen atom revolves in stationary orbit, it
View SolutionIf an electron revolves around a nucleus in a circular orbit of radius R with frequency n, then the magnetic field produced at the center of the nucleus will be
View Solution

