From quantisation of angular momentum one gets for hydrogen atom, the radius of the nth orbit as rn=(n2me)(h2π)2(4πε0e2)
For a hydrogen like atom of atomic number Z,
the radius of the first orbit will be the same
rn will be greater for larger Z values
rn will be smaller for larger Z values
none of these
The correct Answer is:C
To solve the problem regarding the radius of the nth orbit in a hydrogen-like atom with atomic number Z, we will follow these steps:
Step 1: Understand the formula for the radius of the nth orbit in a hydrogen atom
The radius of the nth orbit for a hydrogen atom is given by the formula:
rn=n2me(h2π)2(4πϵ0e2)
where:
- n is the principal quantum number,
- me is the mass of the electron,
- h is Planck's constant,
- ϵ0 is the permittivity of free space,
- e is the charge of the electron.
Step 2: Modify the formula for a hydrogen-like atom
For a hydrogen-like atom with atomic number Z, the radius of the nth orbit can be modified to account for the nuclear charge. The formula becomes:
rn=n2h2ϵ0πmZe2
This indicates that the radius depends on the atomic number Z.
Step 3: Analyze the dependence on atomic number Z
From the modified formula, we can see that as Z increases, the term 1Z indicates that the radius rn will decrease. This means:
- For larger values of Z, the radius of the nth orbit becomes smaller.
Step 4: Conclusion
Thus, we conclude that for a hydrogen-like atom, the radius of the nth orbit decreases as the atomic number Z increases. Therefore, the correct answer to the question is that rn will be smaller for larger Z values.
Final Answer:
The radius rn will be smaller for larger Z values.
---
The radius of the nth orbit for a hydrogen atom is given by the formula:
rn=n2me(h2π)2(4πϵ0e2)
where:
- n is the principal quantum number,
- me is the mass of the electron,
- h is Planck's constant,
- ϵ0 is the permittivity of free space,
- e is the charge of the electron.
For a hydrogen-like atom with atomic number Z, the radius of the nth orbit can be modified to account for the nuclear charge. The formula becomes:
rn=n2h2ϵ0πmZe2
This indicates that the radius depends on the atomic number Z.
From the modified formula, we can see that as Z increases, the term 1Z indicates that the radius rn will decrease. This means:
- For larger values of Z, the radius of the nth orbit becomes smaller.
Thus, we conclude that for a hydrogen-like atom, the radius of the nth orbit decreases as the atomic number Z increases. Therefore, the correct answer to the question is that rn will be smaller for larger Z values.
The radius rn will be smaller for larger Z values.
Topper's Solved these Questions
- ATOMS Book:NCERT FINGERTPS ENGLISHChapter:ATOMS Exercise:Higher order thinking skills
Explore 8 Videos
- ATOMS Book:NCERT FINGERTPS ENGLISHChapter:ATOMS Exercise:NCERT Examplar problems
Explore 7 Videos
- ALTERNATING CURRENT Book:NCERT FINGERTPS ENGLISHChapter:ALTERNATING CURRENT Exercise:Assertion And Reason
Explore 15 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTPS ENGLISHChapter:COMMUNITCATION SYSTEMSExercise:Assertion And Reason
Explore 30 Videos
Similar Questions
Knowledge Check
In a hydrogen atom, the radius of nth bohr orbit is rn. The graph between log (rn/r1) and logn will be
A B
B C
C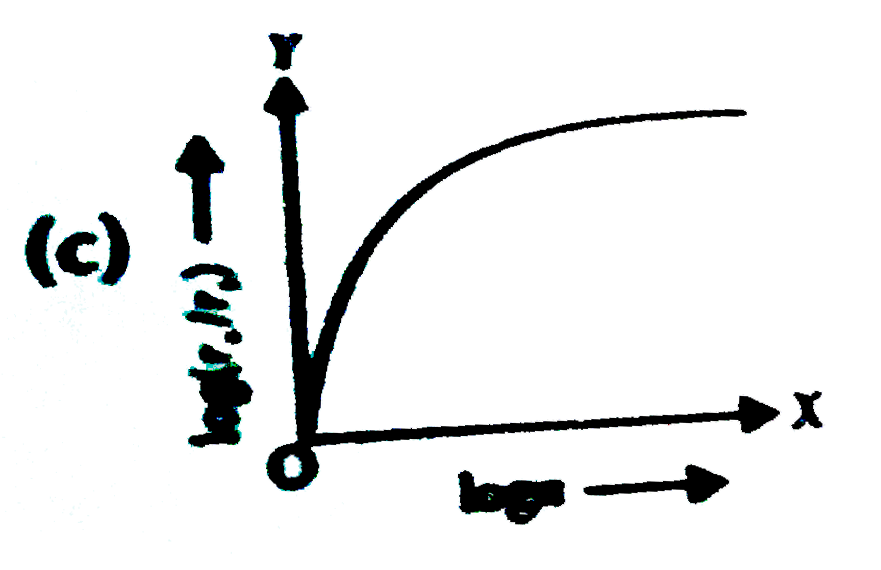 D
D
Derive Bohr's quantisation condition for angular momentum of orbiting electron in hydrogen atom using De Broglie's hypothesis.
View SolutionThe angular momentum of an electron in hydrogen atom is 4h/2π. Kinetic energy this electron is
View SolutionFind variation of angular speed and time period of single
. electron of hydrogen like atoms with n and Z.
View SolutionAssertion The radius of second orbit of hydrogen atom is 2.1Å
Reason Radius of nth orbit of hydrogen atom rn∝n2
View SolutionFor a Bohr atom, angular momentum of an electron is (n = 0, 1,2 .....)
View SolutionThe angular momentum of an electron in a hydrogen atom is proportional to (where n is principle quantum number )
View SolutionThe angular momentum J of the electron in a hydrogen atom is proportional to nth power of r (radius of the orbit) where n is :-
View Solution

