When the state of a gas adiabatically changed from an equilibrium state A to another equilibrium state B an amount of work done on the stystem is 35 J. If the gas is taken from state A to B via process in which the net heat absorbed by the system is 12 cal, then the net work done by the system is (1 cal = 4.19 J)
a. 13.2J
b. 15.4 J
c. 12.6 J
d. 16.8 J
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Work Done on the System
When the gas changes from state A to state B adiabatically, the work done on the system is given as 35 J. Since work is done on the system, we consider this as negative work done by the system. Thus, we can write:
Won=−35J
Step 2: Calculate Change in Internal Energy (ΔU)
For an adiabatic process, the change in internal energy (ΔU) is equal to the negative of the work done on the system:
ΔU=−Won=−(−35J)=35J
Step 3: Convert Heat Absorbed from Calories to Joules
The problem states that the net heat absorbed by the system during the process is 12 cal. We need to convert this to joules using the conversion factor 1cal=4.19J:
Q=12cal×4.19J/cal=50.28J
Step 4: Apply the First Law of Thermodynamics
According to the first law of thermodynamics:
ΔU=Q+W
Where:
- ΔU is the change in internal energy,
- Q is the heat absorbed,
- W is the work done by the system.
We can rearrange this equation to find the work done by the system:
W=ΔU−Q
Step 5: Substitute the Values
Now we can substitute the values we have calculated:
- ΔU=35J
- Q=50.28J
Thus,
W=35J−50.28J=−15.28J
Step 6: Conclusion
The net work done by the system when it is taken from state A to state B via the process in which the net heat absorbed is 12 cal is:
W≈−15.28J
When the gas changes from state A to state B adiabatically, the work done on the system is given as 35 J. Since work is done on the system, we consider this as negative work done by the system. Thus, we can write:
Won=−35J
For an adiabatic process, the change in internal energy (ΔU) is equal to the negative of the work done on the system:
ΔU=−Won=−(−35J)=35J
The problem states that the net heat absorbed by the system during the process is 12 cal. We need to convert this to joules using the conversion factor 1cal=4.19J:
Q=12cal×4.19J/cal=50.28J
According to the first law of thermodynamics:
ΔU=Q+W
Where:
- ΔU is the change in internal energy,
- Q is the heat absorbed,
- W is the work done by the system.
W=ΔU−Q
Now we can substitute the values we have calculated:
- ΔU=35J
- Q=50.28J
W=35J−50.28J=−15.28J
The net work done by the system when it is taken from state A to state B via the process in which the net heat absorbed is 12 cal is:
W≈−15.28J
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HOTs
8 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assertion & Reason
15 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3J is done on the system. If the gas is taken from State A to B via a process in which the net heat absorbed by the system is 9.35cal., How much is the net work done by the system in the later case? (Take 1cal.=4.9J)
View SolutionIn changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3 J is done on the system. If the gas is taken from state A to B, via a process in which the net heat absorbed by the system is 9.35 cal, how much is the net work done by the system in the latter case ?
View Solution
Knowledge Check
In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B an amount of work equal to 22.3 J is done on the system.If the gas is taken from state A to B via a process in which the net heat absorbed by the system is 9.35 cal then the net work done by the system in latter case is
(Take 1 case =4.2 J)A15 JB16 JC17 JD18 JAn ideal gas is taken through cycle A→B→C−A, as shown in Fig. IF the net heat supplied to the gas in the cycle is 5 J, the work done by the gas in the process C→A is
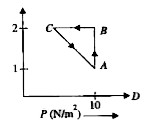 A−5JB−10JC−15JD−20J
A−5JB−10JC−15JD−20J
For a gaseous state if heat supplied to the system is 100 J and work done by the system is 25 J. then internal energy of the system is
View SolutionWhen the state of a system changes from A to B adiabatically the work done on the system is 322 joule. If the state of the same system is changed from A to B by another process, and heat required is 50 calories of heat is required then find work done on the system in this process? (J=4.2J/cal)
View SolutionIf a system undergoes an adiabatic change from state 1 to state 2, the work done by the gas is:
View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from BtoA, the work done on the gas during the process BtoA is 30,J when the gas is taken from A to B the heat absorbed by the gas is 20J Then change in internal energy of the gas in the process A to B is :

View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from BtoA, the work done on the gas during the process BtoA is 30,J when the gas is taken from A to B the heat absorbed by the gas is 20J Then change in internal energy of the gas in the process A to B is :

View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from BtoA, the work done on the gas during the process BtoA is 30,J when the gas is taken from A to B the heat absorbed by the gas is 20J Then change in internal energy of the gas in the process A to B is :

View Solution
