An ideal gas system undergoes an isothermal process, then the work done during the process is
nRTln(V2V1)
nRTln(V1V2)
2nRTln(V2V1)
2nRTln(V1V2)
The correct Answer is:A
To find the work done during an isothermal process for an ideal gas, we can follow these steps:
Step 1: Understand the Isothermal Process
An isothermal process is one in which the temperature of the system remains constant. For an ideal gas, this means that the product of pressure (P) and volume (V) is constant (PV = constant).
Step 2: Write the Expression for Work Done
The work done (W) during a process can be expressed as the integral of pressure with respect to volume:
W=∫V2V1PdV
Step 3: Use the Ideal Gas Law
From the ideal gas law, we know:
PV=nRT
Where:
- n = number of moles of gas
- R = universal gas constant
- T = absolute temperature (constant for isothermal process)
Since PV=nRT is constant, we can express pressure (P) in terms of volume (V):
P=nRTV
Step 4: Substitute Pressure into the Work Integral
Substituting the expression for pressure into the work integral gives:
W=∫V2V1nRTVdV
Step 5: Integrate
The integral of 1V is:
∫1VdV=lnV
Thus, we have:
W=nRT∫V2V11VdV=nRT(lnV)V2V1
Step 6: Apply the Limits of Integration
Applying the limits V1 and V2:
W=nRT(lnV2−lnV1)
Using the properties of logarithms, this can be simplified to:
W=nRTln(V2V1)
Final Result
The work done during the isothermal process is:
W=nRTln(V2V1)
An isothermal process is one in which the temperature of the system remains constant. For an ideal gas, this means that the product of pressure (P) and volume (V) is constant (PV = constant).
The work done (W) during a process can be expressed as the integral of pressure with respect to volume:
W=∫V2V1PdV
From the ideal gas law, we know:
PV=nRT
Where:
- n = number of moles of gas
- R = universal gas constant
- T = absolute temperature (constant for isothermal process)
P=nRTV
Substituting the expression for pressure into the work integral gives:
W=∫V2V1nRTVdV
The integral of 1V is:
∫1VdV=lnV
Thus, we have:
W=nRT∫V2V11VdV=nRT(lnV)V2V1
Applying the limits V1 and V2:
W=nRT(lnV2−lnV1)
Using the properties of logarithms, this can be simplified to:
W=nRTln(V2V1)
The work done during the isothermal process is:
W=nRTln(V2V1)
Topper's Solved these Questions
- THERMODYNAMICSBook:NCERT FINGERTPS ENGLISHChapter:THERMODYNAMICSExercise:HOTs
Explore 8 Videos
- THERMODYNAMICSBook:NCERT FINGERTPS ENGLISHChapter:THERMODYNAMICSExercise:Assertion & Reason
Explore 15 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion And Reason
Explore 10 Videos
- UNITS AND MEASUREMENTSBook:NCERT FINGERTPS ENGLISHChapter:UNITS AND MEASUREMENTSExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Knowledge Check
An ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.
A1.dU=dQB2. dU=-dWC3. dU=0D4. dU=dW
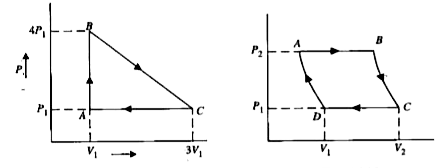
An ideal gas undergoes a thermodynamic process as shown in Fig. The process consists of two isobaric and two isothermal steps. Show that the network done during the whole process is
W(Net)=P1(V2−V1)logeP2P1
View SolutionDerive an expression for the work done during adiabatic process.
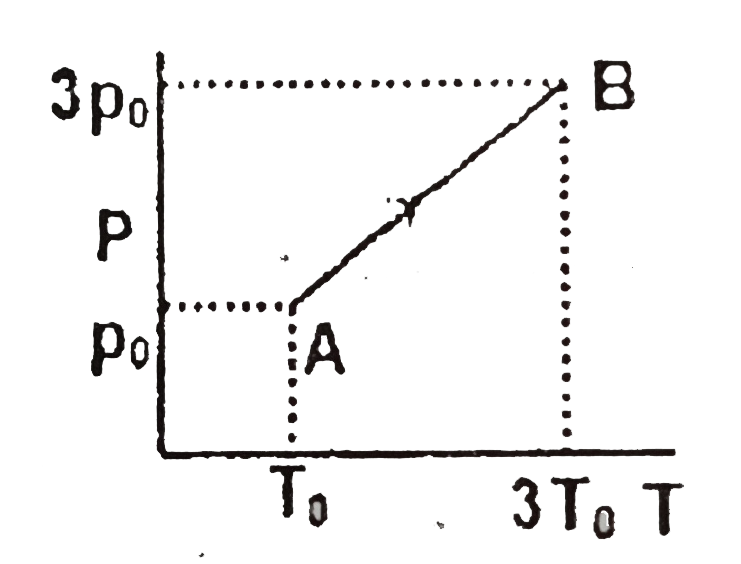
View SolutionTwo moles of a monoatomic ideal gas undergoes a process AB as shown in the figure. Then, find the work done during the process in Joule.
View SolutionIn an isothermal process for an ideal gas
View Solution
An ideal gas undergoes a cyclic process, in which one process is isochoric, one process is isothermal and one process is adiabatic. During the isothermal process, 40 J heat is released by the gas, and during the isochoric process, 80 J heat is absorbed by the gas. if work done by the gas during adiabatic process is W1 and during isothermal process is W2 then the magnitude of W1W2 will be equal to:
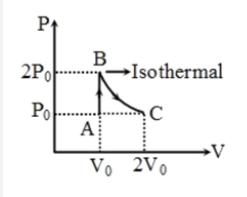
View SolutionAn ideal diatomic gas undergoes a thermodynamic process as shown in the P−V diagram. The process AB is isochoric while the process BC is isothermal. The total heat gein to the gas in the process is nearly (use ln2=0.7)
View Solution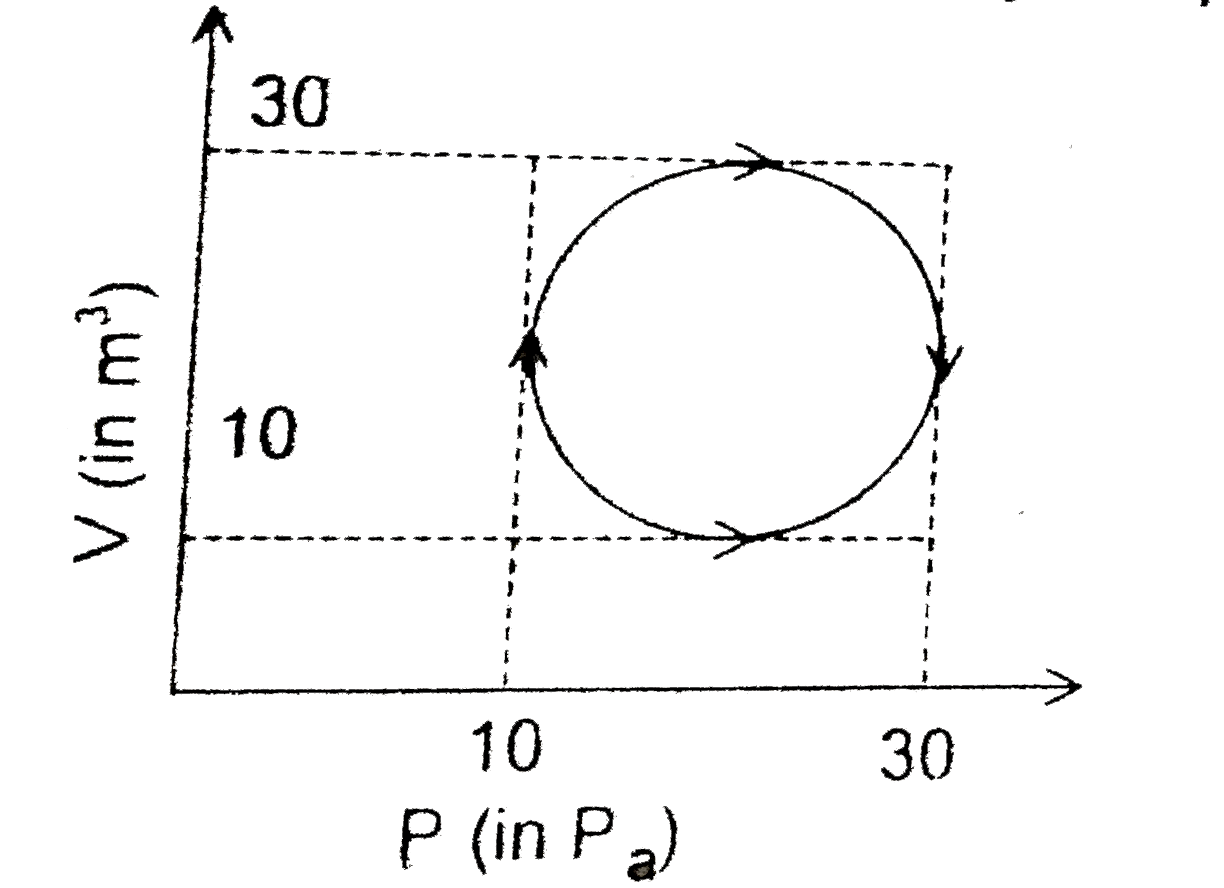
A system works under cyclic process as follow
Heat absorbed during the process is
View Solution
