A ray of light moving along the vector ()undergoes refraction at an interface two media,which is the x-zplane. The refracive index for is and below it is.the unit vector along which the refracted ray moves is:
The correct Answer is:D
To solve the problem step by step, we will apply Snell's law and vector analysis.
Step 1: Identify the incident vector and refractive indices
The incident ray is given as the vector −^i−2^j. The refractive index for the medium above the x-z plane (where y>0) is n1=2, and for the medium below the x-z plane (where y<0), it is n2=√5/2.
Step 2: Normalize the incident vector
To find the unit vector of the incident ray, we need to normalize the incident vector −^i−2^j.
Magnitude=√(−1)2+(−2)2=√1+4=√5
Thus, the unit vector of the incident ray ^i1 is:
^i1=−^i−2^j√5=(−1√5^i−2√5^j)
Step 3: Determine the normal vector
The normal vector at the interface (x-z plane) is directed along the positive y-axis, which can be represented as:
^n=^j
Step 4: Apply Snell's Law in vector form
According to Snell's law in vector form, we have:
n1^i1⋅^n=n2^r1⋅^n
Where ^r1 is the unit vector of the refracted ray. Since the normal vector is ^j, we can simplify the equation:
n1(−2√5)=n2^r1⋅^j
Step 5: Substitute the values of refractive indices
Substituting the values of n1 and n2:
2(−2√5)=√52^r1⋅^j
This simplifies to:
−4√5=√52^r1⋅^j
Step 6: Solve for ^r1⋅^j
Multiplying both sides by 2√5:
−85=^r1⋅^j
Step 7: Express the refracted ray vector
Let the refracted ray be represented as:
^r1=x^i+y^j+z^k
From the previous step, we know that y=−85.
Step 8: Find the relationship between x, y, and z
Using the fact that the refracted ray must also satisfy the condition of being a unit vector:
x2+y2+z2=1
Substituting y:
x2+(−85)2+z2=1
This simplifies to:
x2+6425+z2=1
Step 9: Solve for x and z
Rearranging gives:
x2+z2=1−6425=25−6425=−3925
This indicates that there is no real solution for x and z under these conditions, suggesting that the refracted ray may not exist in the given configuration.
Final Step: Conclusion
The refracted ray's unit vector can be expressed as:
^r1=−4^i+3^j
The unit vector along which the refracted ray moves is:
^r1=−4^i+3^j√(−4)2+32=−4^i+3^j5
The incident ray is given as the vector −^i−2^j. The refractive index for the medium above the x-z plane (where y>0) is n1=2, and for the medium below the x-z plane (where y<0), it is n2=√5/2.
To find the unit vector of the incident ray, we need to normalize the incident vector −^i−2^j.
The normal vector at the interface (x-z plane) is directed along the positive y-axis, which can be represented as:
According to Snell's law in vector form, we have:
Substituting the values of n1 and n2:
Multiplying both sides by 2√5:
Let the refracted ray be represented as:
Using the fact that the refracted ray must also satisfy the condition of being a unit vector:
Rearranging gives:
The refracted ray's unit vector can be expressed as:
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:NCERT EXAMPLAR PROBLEMS
Explore 11 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:ASSERTION AND REASON
Explore 15 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Paper 3
Explore 50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Book:NCERT FINGERTPS ENGLISHChapter:SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A ray of light moving along a vector (3√2ˆi−3ˆj−3ˆk) undergoes refraction at an interface of two media which is y-z plane. The refractive index for x≤0 is 1 while for x≥0 it is √2. Then,
View SolutionThe unit vector along →A=2ˆi+3ˆj is :
View SolutionThe unit vector along →A=2ˆi+3ˆj is :
View SolutionA ray of light travelling along the line x+y=1 is incident on the X - axis and after refraction the other side of the X - axis by turning π/6 by turning away from the X - axis .The equation of the line along which the refracted ray travels is
View SolutionA ray of light is sent along the line 2x−3y=5. After refracting across the line x+y=1 it enters the opposite side after torning by 150 away from the line x+y=1 . Find the equation of the line along which the refracted ray travels.
View SolutionA ray of light is incident on a plane mirror along a vector ˆi+ˆj−ˆk.
The normal on incidence point is along ˆi+ˆj.Find a unit vector along the
reflected ray.
View Solutionx-y plane separates two media, z≥0 contains a medium of refractive index 1 and z≤0 contains a medium of refractive index 2. A ray of light is incident from first medium along a vectorˆi+ˆj−ˆk. Find the unit vector along the refracted ray.
View SolutionIn the diagram shown, light is incident on the interface between media 1 (refractive index n1) and 2 (refractive index n2) at angle slightly greater than the critical angle, and is totally reflected. The light is then also totally reflected at the interface between media 1 and 3 (refractive index n3), after which it travels in a direction opposite to its initial direction, The media must have a refractive indices such that.
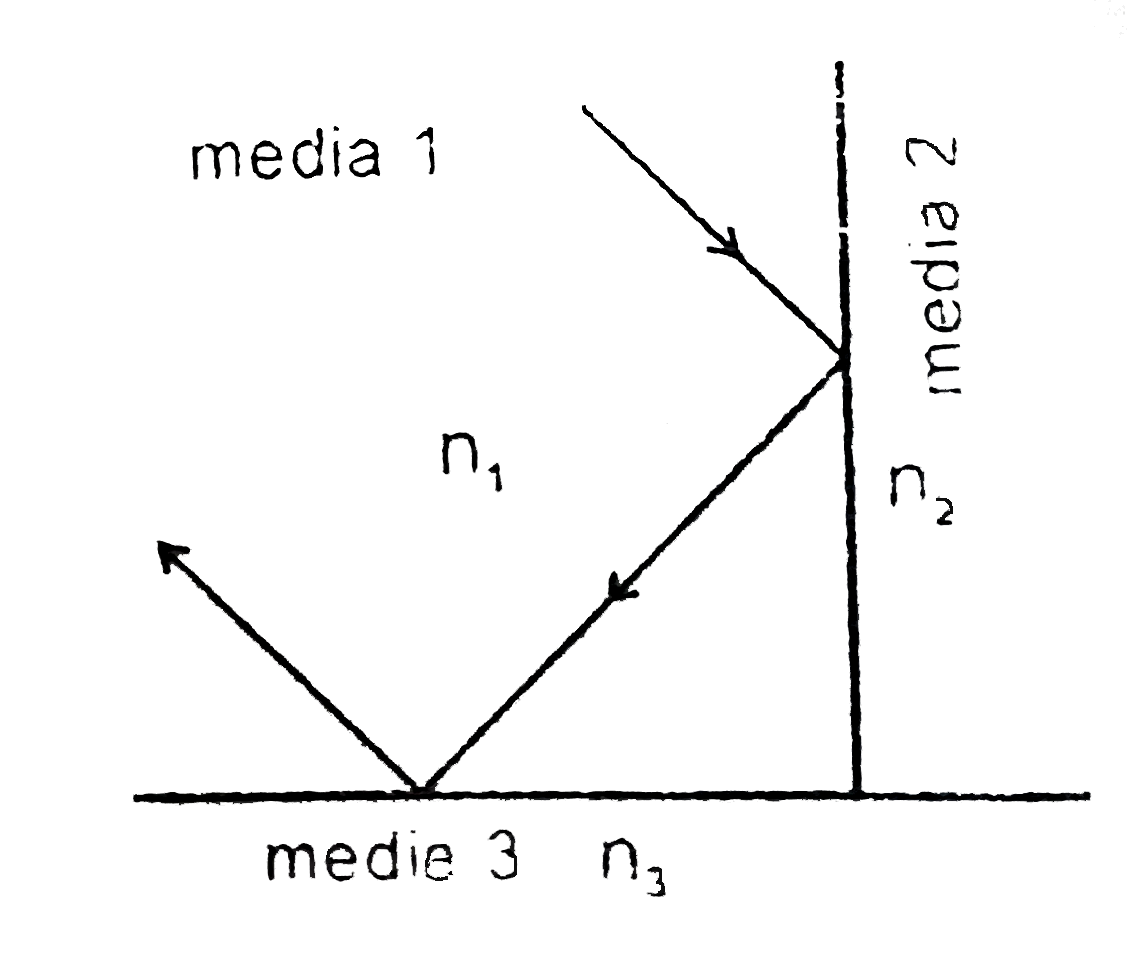 .
.
View SolutionIn the figure shown, the angle made by the light ray with the normal in the medium of refractive index √2 is
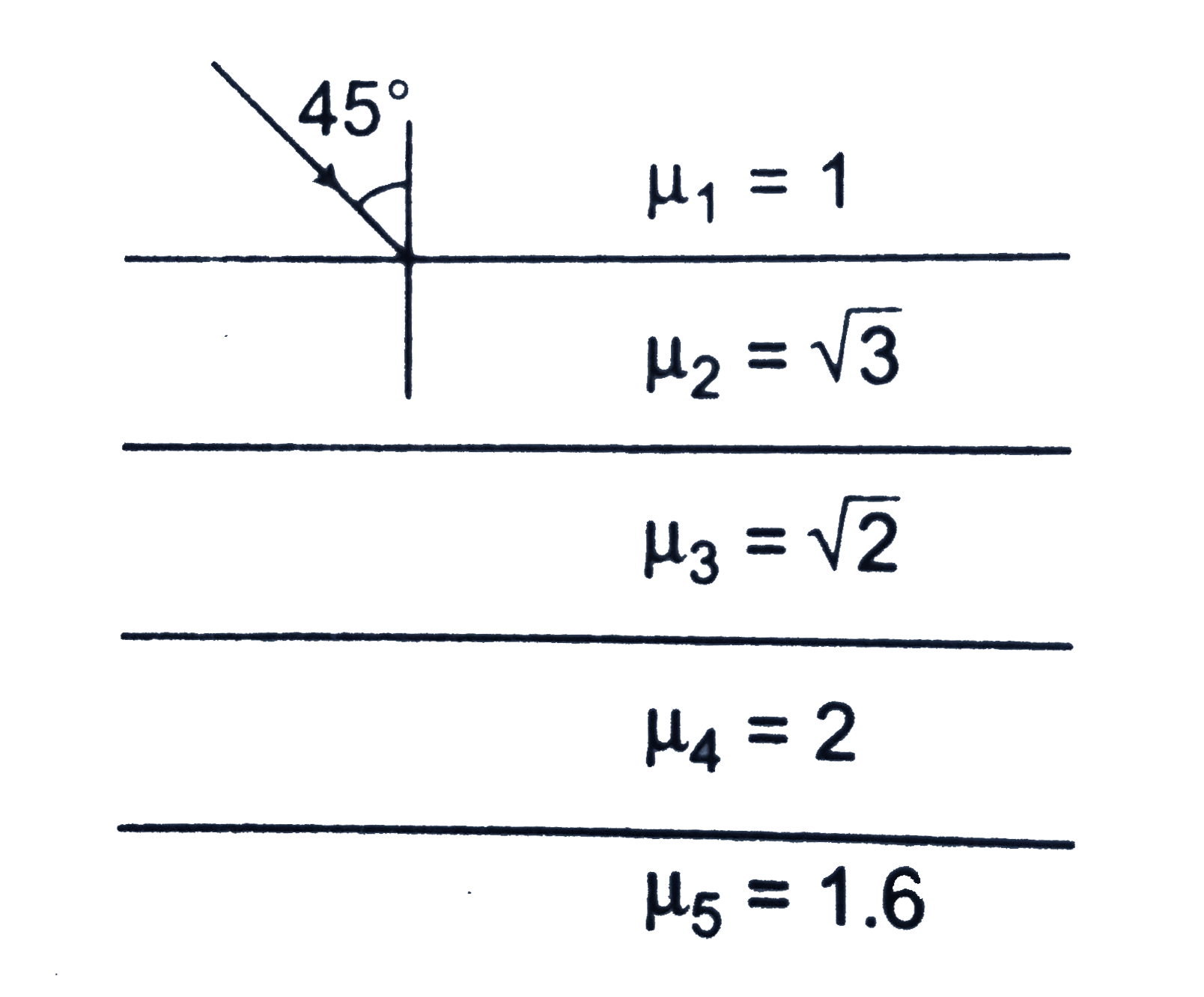
View SolutionFind the angle of deviation suffered by the light ray shown in figure. The refractive index μ=2.0 for the prism material.
View Solution