Two short bar magnets of magnetic moments m each are arranged at the opposite corners of a square of side d such that their centres coincide with thecorners and their axes are parallel. If the like poles are in the same direction, the magnetic induction at any of the other corners of the square is
μ04πmd3
μ04π2md3
μ04πm2d3
μ04πm32d3
The correct Answer is:A
To solve the problem, we need to find the magnetic induction at one of the corners of the square formed by two bar magnets, each with a magnetic moment m. The arrangement has the like poles facing each other. Let's denote the corners of the square as A, B, C, and D, where the magnets are placed at corners A and C, and we want to find the magnetic induction at corner B or D.
1. Understanding the Configuration:
- We have two bar magnets with magnetic moments m placed at opposite corners of a square of side d.
- The magnets are aligned such that their like poles (e.g., north poles) are facing each other.
2. Identify the Points:
- Let’s denote the corners of the square as follows:
- A (where Magnet 1 is located)
- B (where we want to find the magnetic induction)
- C (where Magnet 2 is located)
- D (the other corner)
- We will calculate the magnetic induction at point B due to both magnets.
3. Magnetic Field Due to Each Magnet:
- The magnetic field B1 at point B due to Magnet 1 (at corner A) can be calculated using the formula for the magnetic field along the axial line:
B1=μ04π⋅2md3
- The magnetic field B2 at point B due to Magnet 2 (at corner C) can be calculated using the formula for the magnetic field along the equatorial line:
B2=μ04π⋅md3
4. Direction of Magnetic Fields:
- The magnetic field B1 due to Magnet 1 at point B will point away from the magnet (towards the center of the square).
- The magnetic field B2 due to Magnet 2 at point B will point towards the magnet (since it is an equatorial point).
5. Resultant Magnetic Induction:
- Since B1 points away from Magnet 1 and B2 points towards Magnet 2, the resultant magnetic induction B at point B is given by:
B=B1−B2
- Substituting the values:
B=μ04π⋅2md3−μ04π⋅md3
- Simplifying this expression:
B=μ04π⋅2m−md3=μ04π⋅md3
6. Final Result:
- The magnetic induction at point B is:
B=μ0m4πd3
Conclusion:
The magnetic induction at any of the other corners of the square is given by:
μ0m4πd3
- We have two bar magnets with magnetic moments m placed at opposite corners of a square of side d.
- The magnets are aligned such that their like poles (e.g., north poles) are facing each other.
- Let’s denote the corners of the square as follows:
- A (where Magnet 1 is located)
- B (where we want to find the magnetic induction)
- C (where Magnet 2 is located)
- D (the other corner)
- We will calculate the magnetic induction at point B due to both magnets.
- The magnetic field B1 at point B due to Magnet 1 (at corner A) can be calculated using the formula for the magnetic field along the axial line:
B1=μ04π⋅2md3
- The magnetic field B2 at point B due to Magnet 2 (at corner C) can be calculated using the formula for the magnetic field along the equatorial line:
B2=μ04π⋅md3
- The magnetic field B1 due to Magnet 1 at point B will point away from the magnet (towards the center of the square).
- The magnetic field B2 due to Magnet 2 at point B will point towards the magnet (since it is an equatorial point).
- Since B1 points away from Magnet 1 and B2 points towards Magnet 2, the resultant magnetic induction B at point B is given by:
B=B1−B2
- Substituting the values:
B=μ04π⋅2md3−μ04π⋅md3
- Simplifying this expression:
B=μ04π⋅2m−md3=μ04π⋅md3
- The magnetic induction at point B is:
B=μ0m4πd3
The magnetic induction at any of the other corners of the square is given by:
μ0m4πd3
Topper's Solved these Questions
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - MAGNETISM AND GAUSS S LAW
2 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - THE EARTH S MAGNETISM
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Assertion And Reason
15 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
Similar Questions
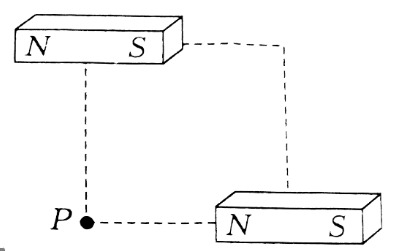
Two short magnets of magnetic moment 1000Am2 are placed as shown at the corners of a square of side 10cm. The net magnetic induction at P is
View SolutionTwo identical short bar magnets of magnetic moment M each are placed at distance r apart in end-on position, then magnetic force between both is
View SolutionThree identical bar magnets each of magnetic moment M are arranged in the form of an equilateral triangle such that at two vertices like poles are in contact. The resultant magnetic moment will be
View SolutionTwo identical bar magnets, each of magnetic moment M, are placed as shown in figure. Magnetic field at point
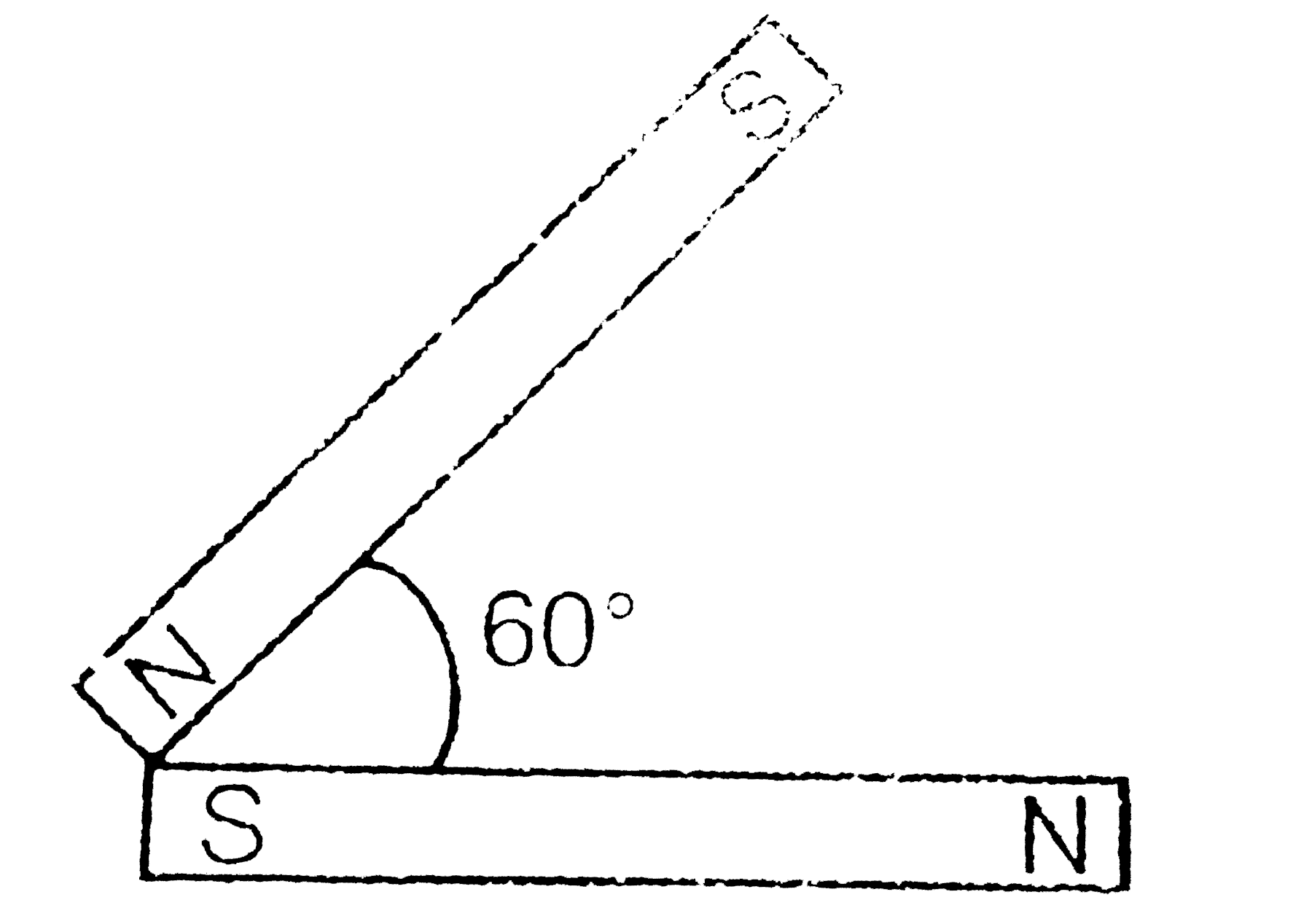
View SolutionTwo identical bar magnets of magnetic moment M each are inclined to 60∘ as shown in figure . The net magnetic moment of the combination in this position , is
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View SolutionFour particles of masses 2,2,4,4 kg are arranged at the corners A,B,C,D of a square ABCD of side 2m as shown in the figure. The perpendicular distance of their centre of mass from the side AB is

View SolutionFour identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
View SolutionThree charges each of +4μC are the corners B, C, D of a square ABCD of side 1m. The electric field at the centre .O. of the square is
View SolutionThere are four solid balls with their centres at the four corners of a square of side a. the mass of each sphere is m and radius is r. Find the moment of inertia of the system about one of the sides of the square
View Solution
