Two metallic plates AandB , each of area 5×10m are placed parallel to each other at a separation of 1 cm . Plate B carries a positive charge of 33.7 pc . A monochromatic beam of light, with photons of energy 5 eV each, starts falling on plate A at t = 0, so that 10 photons fall on it per square meter per second. Assume that one photoelectron is emitted for every 10 incident photons. Also assume that all the emitted photoelectrons are collected by plate B and the work function of plate A remains constant at the value 2 eV . Electric field between the plates at the end of 10 seconds is
5×106
7×107
5×107
9×106
The correct Answer is:C
To solve the problem step by step, we will follow the outlined procedure:
Step 1: Identify the Given Data
- Area of each plate, A=5×10−4m2
- Separation between the plates, d=1cm=0.01m
- Charge on plate B, Q=33.7pC=33.7×10−12C
- Energy of each photon, E=5eV
- Work function of plate A, ϕ=2eV
- Rate of incident photons, n=10photons/m2/s
- Time, t=10s
Step 2: Calculate the Total Number of Incident Photons
The total number of photons incident on plate A in 10 seconds can be calculated as follows:
Total photons=Rate of incident photons×Area×Time
Total photons=10photons/m2/s×5×10−4m2×10s
=10×5×10−4×10=5×10−3photons
Step 3: Calculate the Number of Photoelectrons Emitted
According to the problem, one photoelectron is emitted for every 10 incident photons. Therefore, the number of photoelectrons emitted can be calculated as:
Number of photoelectrons=Total photons10
=5×10−310=5×10−4photoelectrons
Step 4: Calculate the Charge of the Emitted Photoelectrons
The charge of the emitted photoelectrons can be calculated using the charge of an electron, e=1.6×10−19C:
Total charge=Number of photoelectrons×e
=5×10−4×1.6×10−19C
=8×10−24C
Step 5: Calculate the Total Charge on Plate B
The total charge on plate B after collecting the emitted photoelectrons can be calculated as:
Total charge on B=Q+Charge of emitted photoelectrons
=33.7×10−12+8×10−24≈33.7×10−12C(since 8×10−24 is negligible)
Step 6: Calculate the Electric Field Between the Plates
The electric field E between two plates is given by:
E=Qε0A
Where ε0=8.85×10−12C2/N m2 is the permittivity of free space. Substituting the values:
E=33.7×10−128.85×10−12×5×10−4
Calculating this gives:
E≈33.78.85×5×104≈0.76×104N/C=7600N/C
Final Answer
The electric field between the plates at the end of 10 seconds is approximately 7600N/C.
---
- Area of each plate, A=5×10−4m2
- Separation between the plates, d=1cm=0.01m
- Charge on plate B, Q=33.7pC=33.7×10−12C
- Energy of each photon, E=5eV
- Work function of plate A, ϕ=2eV
- Rate of incident photons, n=10photons/m2/s
- Time, t=10s
The total number of photons incident on plate A in 10 seconds can be calculated as follows:
Total photons=Rate of incident photons×Area×Time
Total photons=10photons/m2/s×5×10−4m2×10s
=10×5×10−4×10=5×10−3photons
According to the problem, one photoelectron is emitted for every 10 incident photons. Therefore, the number of photoelectrons emitted can be calculated as:
Number of photoelectrons=Total photons10
=5×10−310=5×10−4photoelectrons
The charge of the emitted photoelectrons can be calculated using the charge of an electron, e=1.6×10−19C:
Total charge=Number of photoelectrons×e
=5×10−4×1.6×10−19C
=8×10−24C
The total charge on plate B after collecting the emitted photoelectrons can be calculated as:
Total charge on B=Q+Charge of emitted photoelectrons
=33.7×10−12+8×10−24≈33.7×10−12C(since 8×10−24 is negligible)
The electric field E between two plates is given by:
E=Qε0A
Where ε0=8.85×10−12C2/N m2 is the permittivity of free space. Substituting the values:
E=33.7×10−128.85×10−12×5×10−4
Calculating this gives:
E≈33.78.85×5×104≈0.76×104N/C=7600N/C
The electric field between the plates at the end of 10 seconds is approximately 7600N/C.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - EXEMPLAR PROBLEMS
8 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSERTION & REASON CORNER
15 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - DAVISSON AND GERMER EXPERIMENT
3 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Two metallic plate A and B , each of area 5×10−4m2, are placed parallel to each at a separation of 1cm plate B carries a positive charge of 33.7×10−12C A monocharonatic beam of light , with photoes of energy 5eV each , starts falling on plate A at t=0 so that 1016 photons fall on it per square meter per second. Assume that one photoelectron is emitted for every 106 incident photons fall on it per square meter per second. Also assume that all the emitted photoelectrons are collected by plate B and the work function of plate A remain constant at the value 2eV Determine
(a) the number of photoelectrons emitted up to i=10s,
(b) the magnitude of the electron field between the plate A and B at i=10s,and
(c ) the kinetic energy of the most energotic photoelectrons emitted at i=10s whenit reaches plate B
Negilect the time taken by the photoelectrons to reach plate B Take ε0=8.85×10−12C2N−m2
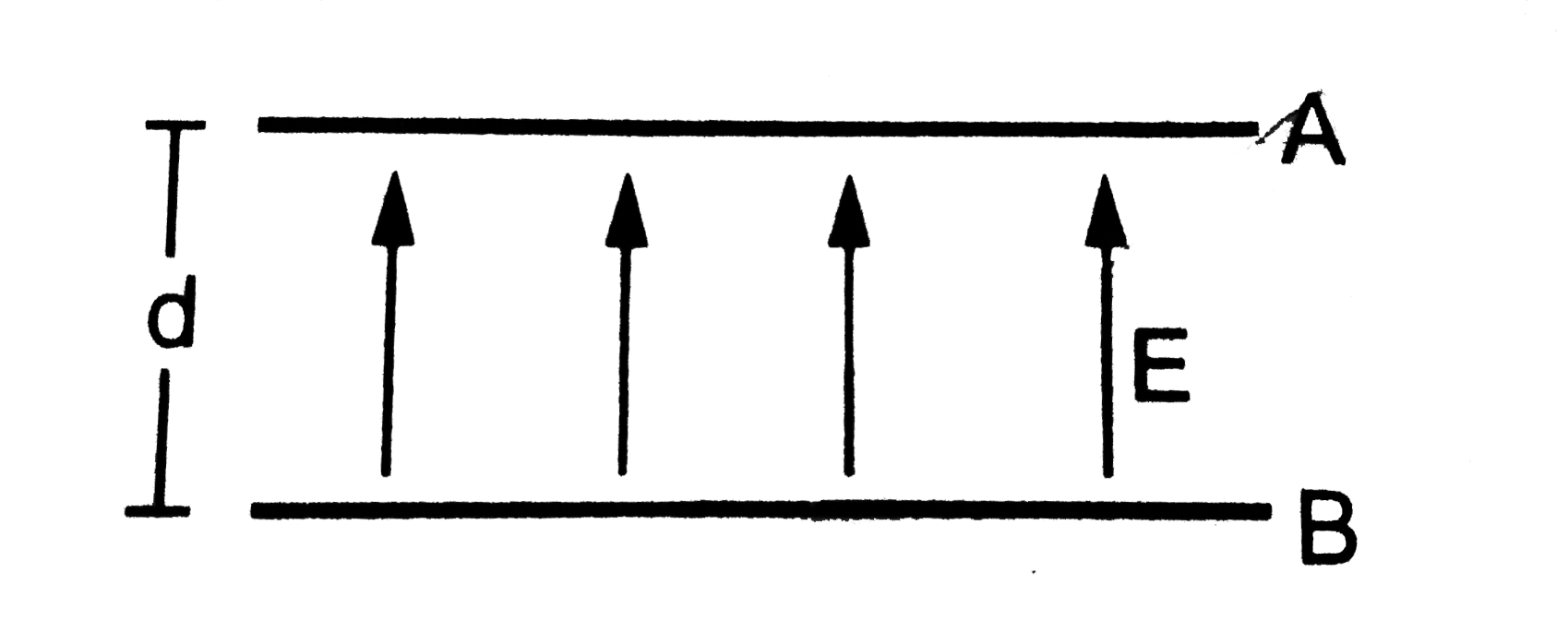
View SolutionFigure shows two metallic plates A and B placed parallel to each other at a seperation d. A uniform electric field E exists between the plates in the direction from plate B to plate A. Find the potential difference between the plates.
View SolutionTwo conducting plates M and N, each having large surface area A (on one side), are placed parallel to each other in figure. The plate M is given charge Q1 and N, charge Q2(<Q1). Then

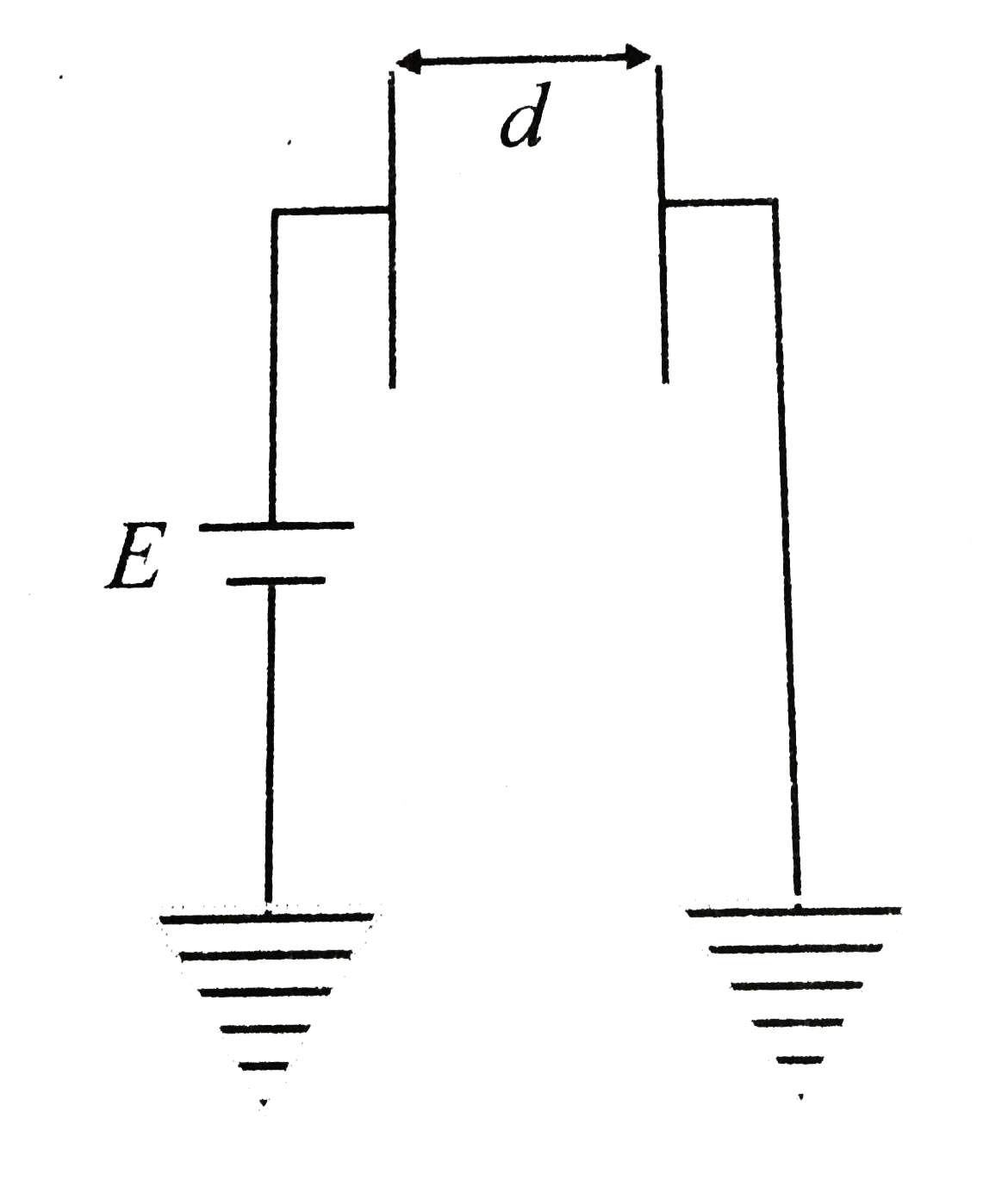
View SolutionTwo plates, each of area A, are placed parallel to each other at a distance d. One plate is connected to a battery of emf E and its negative is earthed. The other plate is also earthed. The charge drawn by plate is
View SolutionThree identical large metallic plates are placed parallel to each other at a very small separation as shown in. The central plate is give a charge Q. What amount of charge will flow to earth when the key is pressid?
 .
.
View SolutionAt t=O, light of intensity 1012 photons/s−m2 of energy 6eV per photon starts falling on a plate with work founction 2.5eV If area of the plate is 2×10−4m2 and for every 105 photons one photoelectron is emitted, charge on the plate at t=25 s is
View SolutionA small plate of a metal is placed at a distance of 2m from a monochromatic light source of wavelenght 4.8×10−7m and power 1.0 Watt. The light falls normally on the plate. Find the number of photons striking the metal plate per square metre per second.
View SolutionFind the charge on each plate given area of each plate is A and separation between two consecutive plates is d.

View SolutionThree plates A,B and C each of area 0.1m2 are separated by 0.885mm from each other as shown in the figure. A 10V battery is used to charge the system. The enegry stored in the system is

View SolutionTwo large conducting plates are placed parallel to each other with a separation of 2.00 cm betweeen them. An electron starting from rest near one of the plates reaches the other plate in 2.00 microseconds. Find the surface charge density on the inner surfaces.
View Solution
