Unpolarized light is incident on a plane glass surface. The angle of incidence so that reflected and refracted rays and perpendicular to each other, then
taniβ=μ2
taniβ=μ
siniβ=μ
cosiβ=μ
The correct Answer is:B
To solve the problem, we need to find the relationship between the angle of incidence (I) at which the reflected and refracted rays are perpendicular to each other when unpolarized light strikes a plane glass surface.
1. Understanding the Situation:
- We have unpolarized light incident on a plane glass surface.
- The light will be partially reflected and partially refracted at the surface.
2. Condition for Perpendicular Rays:
- We need to find the angle of incidence (I) such that the reflected ray and the refracted ray are perpendicular to each other.
- This means that if the angle of reflection is R and the angle of refraction is r, then R + r = 90°.
3. Using Snell's Law:
- According to Snell's Law, we have:
n1sinI=n2sinr
- Here, n1 is the refractive index of air (approximately 1), and n2 is the refractive index of glass.
4. Relating Angles:
- Since R + r = 90°, we can express r as:
r=90°−R
- Therefore, we can substitute this into Snell's Law:
sinr=sin(90°−R)=cosR
- This gives us:
n1sinI=n2cosR
5. Using the Reflection Law:
- From the law of reflection, we know that the angle of reflection R is equal to the angle of incidence I:
R=I
- Substituting this into our earlier equation gives:
n1sinI=n2cosI
6. Rearranging the Equation:
- Rearranging the equation leads to:
sinIcosI=n2n1
- This simplifies to:
tanI=n2n1
7. Identifying the Polarizing Angle:
- The angle of incidence I at which the reflected and refracted rays are perpendicular is known as the polarizing angle (θp). Therefore, we can write:
tanθp=n2
- If we denote the refractive index of air as n1=1, we have:
tanθp=n2
Final Relation:
Thus, the relationship we are looking for is:
tanIb=n
where Ib is the angle of incidence at which the reflected and refracted rays are perpendicular.
- We have unpolarized light incident on a plane glass surface.
- The light will be partially reflected and partially refracted at the surface.
- We need to find the angle of incidence (I) such that the reflected ray and the refracted ray are perpendicular to each other.
- This means that if the angle of reflection is R and the angle of refraction is r, then R + r = 90°.
- According to Snell's Law, we have:
n1sinI=n2sinr
- Here, n1 is the refractive index of air (approximately 1), and n2 is the refractive index of glass.
- Since R + r = 90°, we can express r as:
r=90°−R
- Therefore, we can substitute this into Snell's Law:
sinr=sin(90°−R)=cosR
- This gives us:
n1sinI=n2cosR
- From the law of reflection, we know that the angle of reflection R is equal to the angle of incidence I:
R=I
- Substituting this into our earlier equation gives:
n1sinI=n2cosI
- Rearranging the equation leads to:
sinIcosI=n2n1
- This simplifies to:
tanI=n2n1
- The angle of incidence I at which the reflected and refracted rays are perpendicular is known as the polarizing angle (θp). Therefore, we can write:
tanθp=n2
- If we denote the refractive index of air as n1=1, we have:
tanθp=n2
Thus, the relationship we are looking for is:
tanIb=n
where Ib is the angle of incidence at which the reflected and refracted rays are perpendicular.
Topper's Solved these Questions
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - HIGHER ORDER THINKING SKILLS
8 Videos
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - NCERT EXEMPLAR PROBLEMS
5 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Unpolarized light is incident on a plane glass surface. What should be the angle of incidence so that the reflected and refracted rays are perpendicular to eachother ?
View SolutionUnpolarized light is incident on a plane glass surface having refractive index . The angle of incidence at which reflected and refracted rays would become perpendicular to each other is :
View Solution
Knowledge Check
A ray of light in incident on a glass plate at an angle of 60∘. What is the refractive index of glass if the reflected and refracted rays are perpendicular to each other?
A12B√32C32D√3
Unpolarised light is incident from air on a plane surface of a material of refractive index μ. At a particular angle of incidence i, it is found that the reflected and refracted rays are perpendicular to each other. Which of the following options is correct for this situation?
View SolutionUnpolarised light is incident from air on a plane surface of a material of refractive index .μ.. At a particular angle of incidence .I., it is found that the reflected and refracted rays are perpendicular to each other. Which of the following options is correct for this situation?
View SolutionA : When an unpolarised light is incident on a glass plate at Brewster angle, the reflected ray and refracted ray are matually perpendicular.
R : The refractive index of glass is equal to sine of the angle of polarisation.
View SolutionA ray of light is incident on a transparent glass slab of refractive index √3. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence?
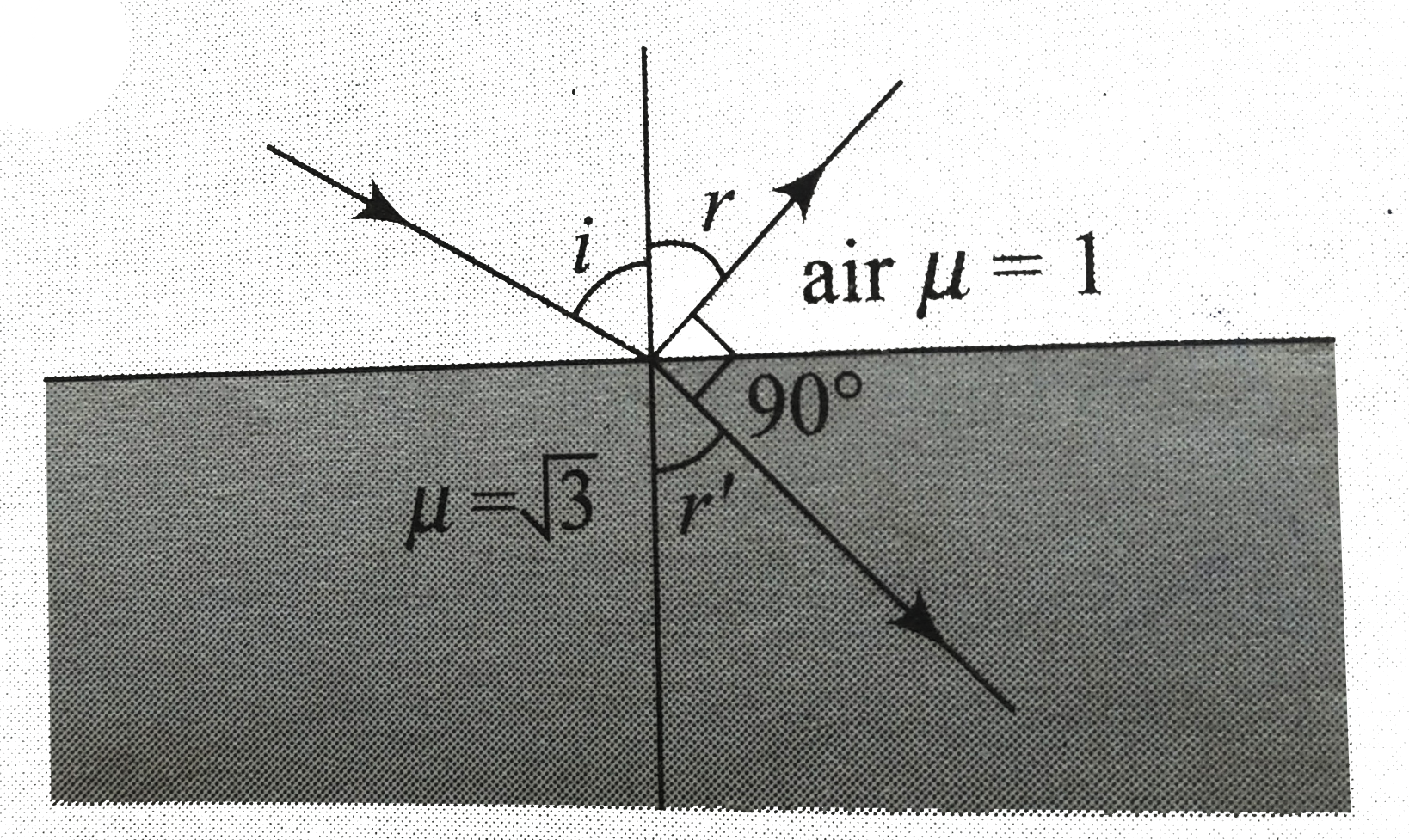
View SolutionA ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
View SolutionA light ray is incident normally on a plane mirror.
What is the angle of incidence?
View SolutionStatement I: A light ray is incident on a glass slab. Some portion of it is reflected and some is refracted. Refracted and reflected rays are always perpendicular to each other.
Statement II: Angle of incidence is equal to angle of reflection.

View Solution
