For the same objective, what is the ratio of the least separation between two points to be distinguished by a microscope for light of 5000 Ã… and electrons accelerated through 100 V used as an illuminating substance?
3075
3575
4075
5075
The correct Answer is:C
To solve the problem, we need to find the ratio of the least separation between two points that can be distinguished by a microscope using light of wavelength 5000 Å (angstroms) and electrons accelerated through 100 V.
1. Understanding the Limit of Resolution:
The limit of resolution (d) for a microscope is given by the formula:
d=λ2sinθ
Since we are using the same objective, the angle θ is the same for both cases, which means we can express the ratio of the least separations (d1 and d2) in terms of their wavelengths:
d1d2=λ1λ2
2. Identifying the Wavelengths:
- For the light microscope, the wavelength λ1 is given as 5000 Å.
- For the electrons, we need to calculate the de Broglie wavelength λ2.
3. Calculating the de Broglie Wavelength:
The de Broglie wavelength λ of a particle is given by:
λ=hp
where h is Planck's constant and p is the momentum of the particle. The momentum p can be expressed in terms of kinetic energy K:
p=√2mK
For electrons accelerated through a potential V, the kinetic energy K is given by:
K=qV
where q is the charge of the electron (approximately 1.6×10−19C) and V is the accelerating voltage (100 V).
4. Substituting Values:
The kinetic energy for the electron is:
K=(1.6×10−19C)(100V)=1.6×10−17J
Now substituting this into the momentum equation:
p=√2m(1.6×10−17)
where the mass m of an electron is approximately 9.11×10−31kg.
5. Calculating the Momentum:
p=√2×(9.11×10−31)×(1.6×10−17)≈√2.91×10−47≈5.39×10−24kg⋅m/s
6. Calculating the de Broglie Wavelength:
Using h≈6.63×10−34J⋅s:
λ2=hp=6.63×10−345.39×10−24≈1.23×10−10m=1.23×1010Å
7. Finding the Ratio of Least Separations:
Now we can find the ratio:
d1d2=λ1λ2=5000Å1.23×1010Å≈4075
Final Answer:
The ratio of the least separation between two points to be distinguished by a microscope for light of 5000 Å and electrons accelerated through 100 V is approximately 4075.
The limit of resolution (d) for a microscope is given by the formula:
d=λ2sinθ
Since we are using the same objective, the angle θ is the same for both cases, which means we can express the ratio of the least separations (d1 and d2) in terms of their wavelengths:
d1d2=λ1λ2
- For the light microscope, the wavelength λ1 is given as 5000 Å.
- For the electrons, we need to calculate the de Broglie wavelength λ2.
The de Broglie wavelength λ of a particle is given by:
λ=hp
where h is Planck's constant and p is the momentum of the particle. The momentum p can be expressed in terms of kinetic energy K:
p=√2mK
For electrons accelerated through a potential V, the kinetic energy K is given by:
K=qV
where q is the charge of the electron (approximately 1.6×10−19C) and V is the accelerating voltage (100 V).
The kinetic energy for the electron is:
K=(1.6×10−19C)(100V)=1.6×10−17J
Now substituting this into the momentum equation:
p=√2m(1.6×10−17)
where the mass m of an electron is approximately 9.11×10−31kg.
p=√2×(9.11×10−31)×(1.6×10−17)≈√2.91×10−47≈5.39×10−24kg⋅m/s
Using h≈6.63×10−34J⋅s:
λ2=hp=6.63×10−345.39×10−24≈1.23×10−10m=1.23×1010Å
Now we can find the ratio:
d1d2=λ1λ2=5000Å1.23×1010Å≈4075
The ratio of the least separation between two points to be distinguished by a microscope for light of 5000 Å and electrons accelerated through 100 V is approximately 4075.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - HIGHER ORDER THINKING SKILLS8videos
WAVE OPTICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - NCERT EXEMPLAR PROBLEMS5videos
WAVE OPTICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason15videos
SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS
Similar Questions
For the same objective, the ratio of least separation between two points to be distinguished by a microscope for light of 5000Å and electrons accelerated through 100V used as illuminating substance is __________ (nearly)
View SolutionFor the same objective, the ratio of least separation between two points to be distiguised by a microscope for light of 5000Å and electrons acclerated through 100V used as illuminating substance is __________ (neraly)
View Solution
Knowledge Check
- Question 1 - Select One
Two points separated by a distance of 0.1mm can just be resolved in a microscope when a light of wavelength 6000Å is used. If the light of wavelength 4800Å is used this limit of resolution becomes
A0.8 mmB0.12 mmC0.1 mmD0.08 mm
What is de-Broglie wavelength of the electron accelerated through a potential difference of 100V?
View SolutionWhat possibly can be the ratio of the de Broglie wavelength for two electrons each having zero initial energy and accelerated through 50 volts and 200 volts?
View SolutionA wave travelling along the length of a string is shown in Fig. 14.4.12. Using the scale on the given axis, find
(i) The amplitude of the wave
(ii) The wavelength of the wave
(iii) If the frequency of the wave is 10 Hz, What is the speed of the wave?
(iv) What is the initial phase of the wave ?
(v) What is the phase difference between two points separated by a distance 10 cm ?
(vi) If this wave is made to travel through water what is the wavelength of the wave, if the speed of, the waves in water is 10 m/s.
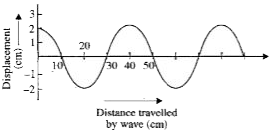 View Solution
View SolutionThe diameter of human eye lens is 2mm. What should be the minimum separation between two points situated at 50m from eye, to resolve tham. Take wavelength of light =5000Å.
View SolutionThe diameter of human eye lens is 2mm. What should be the minimum separation between two points situated at 50m from eye, to resolve tham. Take wavelength of light =5000Å.
View SolutionThe value of numerical aperature of the objective lens of a microscope is 1.25 if light of wavelength 5000 Å is used the minimum separation between two points to be seen as distinct, will be
View SolutionThe heat of neutralization for a strong acid by a strong base is a constant
View Solution
