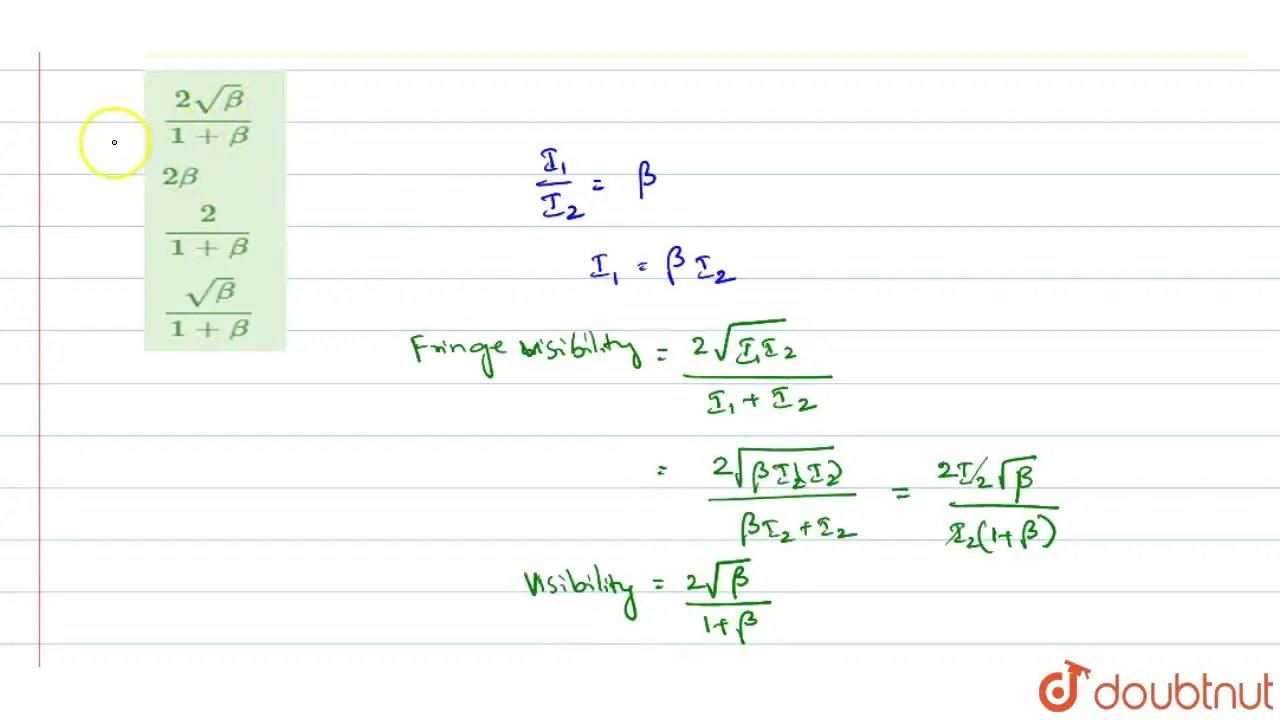The two coherent sources with intensity ratio produce interference. The fringe visibility will be
The correct Answer is:A
Fringe visibility is given by
Related Playlists
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - HIGHER ORDER THINKING SKILLS8videos
WAVE OPTICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - NCERT EXEMPLAR PROBLEMS5videos
WAVE OPTICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason15videos
SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS
Similar Questions
Two coherent sources of light of intensity ratio β produce interference pattern. Prove that in the interferencepattern
Imax−IminImax+(Imin)=2√β1+β
where Imax and Imin are maximum and mininum intensities in the resultant wave.View SolutionThe intensity ratio of two coherent sources of light is p. They are interfering in some region and produce interference patten. Then the fringe visibility is
View SolutionTwo coherent sources of intensities I1 and I2 produce an interference pattern. The maximum intensity in the interference pattern will be
View SolutionIf the intensity of the waves obvserved by two coherent sources is 1. Then the intensity of resultant waves in constructive interferences will be:
View SolutionIf interference is complete or cent percent then the frequency of observed crossover will be
View SolutionTwo coherent sources of intensity ratio β2 interfere. Then, the value of (Imax−Imin)/(Imax+Imin) is
View SolutionTwo coherent light beams of intensities I and 4I produce interference pattern. The intensity at a point where the phase difference is zero, will b:
View SolutionThe interference pattern is obtained with two coherent light sources of intensity ration n. In the interference pattern, the ratio
Imax−IminImax+Imin will beView SolutionTwo coherent sources of different intensities send waves which interfere. The ratio of maximum intensity to the minimum intensity is 25. The intensities of the sources are in the ratio
View SolutionThe interference pattern is obtained with two coherent light sources of intensity ratio n. In the interference patten, the ratio Imax−IminImax+Imin will be
View Solution