The internal energy of one gram of helium at 100 K and one atmospheric pressure is
100 J
1200 J
300 J
500 J
The correct Answer is:C
To find the internal energy of one gram of helium at 100 K and one atmospheric pressure, we can follow these steps:
Step 1: Understand the formula for internal energy
The internal energy (U) of an ideal gas can be calculated using the formula:
U=32nRT
where:
- n is the number of moles,
- R is the universal gas constant (approximately 8.31 J/mol·K),
- T is the temperature in Kelvin.
Step 2: Calculate the number of moles of helium
The molar mass of helium (He) is approximately 4 g/mol. Since we have 1 gram of helium, we can calculate the number of moles (n) as follows:
n=mass of heliummolar mass of helium=1 g4 g/mol=14 moles
Step 3: Substitute values into the internal energy formula
Now that we have the number of moles, we can substitute n, R, and T into the internal energy formula:
U=32(14)RT
Substituting R=8.31 J/mol⋅K and T=100 K:
U=32(14)×8.31×100
Step 4: Simplify the calculation
Calculating step-by-step:
1. Calculate 32×14=38.
2. Now substitute this into the equation:
U=38×8.31×100
3. First, calculate 8.31×100=831.
4. Then, calculate 38×831=311.625.
Step 5: Round off the result
Since the question does not require a decimal point, we can round 311.625 to 312 joules.
Final Answer
Thus, the internal energy of one gram of helium at 100 K and one atmospheric pressure is approximately:
U≈312 joules
The internal energy (U) of an ideal gas can be calculated using the formula:
U=32nRT
where:
- n is the number of moles,
- R is the universal gas constant (approximately 8.31 J/mol·K),
- T is the temperature in Kelvin.
The molar mass of helium (He) is approximately 4 g/mol. Since we have 1 gram of helium, we can calculate the number of moles (n) as follows:
n=mass of heliummolar mass of helium=1 g4 g/mol=14 moles
Now that we have the number of moles, we can substitute n, R, and T into the internal energy formula:
U=32(14)RT
Substituting R=8.31 J/mol⋅K and T=100 K:
U=32(14)×8.31×100
Calculating step-by-step:
1. Calculate 32×14=38.
2. Now substitute this into the equation:
U=38×8.31×100
3. First, calculate 8.31×100=831.
4. Then, calculate 38×831=311.625.
Since the question does not require a decimal point, we can round 311.625 to 312 joules.
Thus, the internal energy of one gram of helium at 100 K and one atmospheric pressure is approximately:
U≈312 joules
Topper's Solved these Questions
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:SPECIFIC CEAT CAPACITY
Explore 13 Videos
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:HOTS
Explore 10 Videos
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:Kinetic Theory of An Ideal Gas
Explore 18 Videos
- GRAVITATIONBook:NCERT FINGERTPS ENGLISHChapter:GRAVITATIONExercise:Assertion And Reason
Explore 15 Videos
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
The internal energy of one mole of ideal gas is
View SolutionThe internal energy of one mole of the diatomic gas at 200 K is
View SolutionThe internal energy of one mole mono-atomic gas is
View SolutionWhat will be the volume occupied by 2 gm of hydrogen at 300 K and 4 atmospheric pressure if at 273 k and 1 atmospheric pressure the gas occupies 22.4 L.
View SolutionOne atmosphere is equal to
View SolutionCalculate the change in internal energy of 3.0 mol of helium gas when its temperature is increased by 2.0K.
View SolutionWhich of the following volume (V) –temperature (T) plots represents the behaviour of one mole of an ideal gas at one atmospheric pressure?
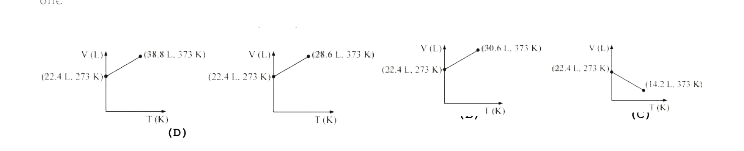
View SolutionDuring the melting of a slab of ice at 273K at atmospheric pressure,
View SolutionDuring the melting of a slab of ice at 273K at atmospheric pressure,
View SolutionDuring the melting of a slab of ice at 273K at atmospheric pressure,
View Solution

