Two opposite forcesF1=120N and F2=80N act on an elastic plank of modulus of elasticity Y=2x1011N/m2 and length l=1m placed over a smooth horizontal surface. The cross-sectional area of the plank is S=0.5m2. The change in length of the plank is x×10−11m. Find the value of x.
A. 100
B. 150
C. 200
B. 1.1
The correct Answer is:A
To solve the problem, we will use the formula for Young's modulus and the relationship between stress, strain, and change in length. Here are the steps:
Step 1: Calculate the net force acting on the plank
The net force F acting on the plank is the difference between the two forces:
F=F1−F2=120N−80N=40N
Step 2: Calculate the stress on the plank
Stress σ is defined as force per unit area:
σ=FS
Substituting the values:
σ=40N0.5m2=80N/m2
Step 3: Calculate the strain in the plank
Strain ϵ is defined as the change in length per unit length:
ϵ=Δxl
Where Δx is the change in length and l is the original length of the plank.
Step 4: Relate stress and strain using Young's modulus
Young's modulus Y is defined as the ratio of stress to strain:
Y=σϵ
Rearranging gives:
ϵ=σY
Step 5: Substitute the values into the strain formula
Substituting the values of stress and Young's modulus:
ϵ=80N/m22×1011N/m2=4×10−10
Step 6: Calculate the change in length Δx
Now we can find Δx using the strain:
Δx=ϵ⋅l=4×10−10⋅1m=4×10−10m
Step 7: Express Δx in the required form
The problem states that the change in length is x×10−11m. We can express our result as:
Δx=40×10−11m
Thus, x=40.
Final Answer
The value of x is:
40
The net force F acting on the plank is the difference between the two forces:
F=F1−F2=120N−80N=40N
Stress σ is defined as force per unit area:
σ=FS
Substituting the values:
σ=40N0.5m2=80N/m2
Strain ϵ is defined as the change in length per unit length:
ϵ=Δxl
Where Δx is the change in length and l is the original length of the plank.
Young's modulus Y is defined as the ratio of stress to strain:
Y=σϵ
Rearranging gives:
ϵ=σY
Substituting the values of stress and Young's modulus:
ϵ=80N/m22×1011N/m2=4×10−10
Now we can find Δx using the strain:
Δx=ϵ⋅l=4×10−10⋅1m=4×10−10m
The problem states that the change in length is x×10−11m. We can express our result as:
Δx=40×10−11m
Thus, x=40.
The value of x is:
40
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:NCERT
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:CORNER
Explore 15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
Explore 8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT Exemplar
Explore 5 Videos
- MOTION IN A PLANE Book:NCERT FINGERTPS ENGLISHChapter:MOTION IN A PLANE Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Knowledge Check
The area of a cross-section of steel wire is 0.1cm−2 and Young's modulus of steel is 2x1011Nm−2. The force required to stretch by 0.1% of its length is
A1000 NB2000 NCÂ 4000 ND5000N
A sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionYoung.s modulus of a wire is 2×1011N/m2. If a stress of 2 x 108 N/m2 is applied at the free end of a wire, find the strain in the wire.
View SolutionA rubber pipe of density 1.5×103N/m2 and Young's modulus 5×106N/m2 is suspended from the roof. The length of the pipe is 8m. What will be the change in length due to its own weight.
View SolutionA block of mass'm' it kept over the smooth surface of the plank of mass M. the plank of length l is kept over the smooth horizontal surface. A constant horizontal force F is applied onto the plank as shown in figure. Calculate the time after which the block falls off the plank?

View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :
View SolutionWhen a force is applied on a wire of uniform cross-sectional area 3×10−6m2 and length 4 m, the increase in length is 1mm. Energy stored in it will be (Y=2×1011Nm2)
View SolutionA block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
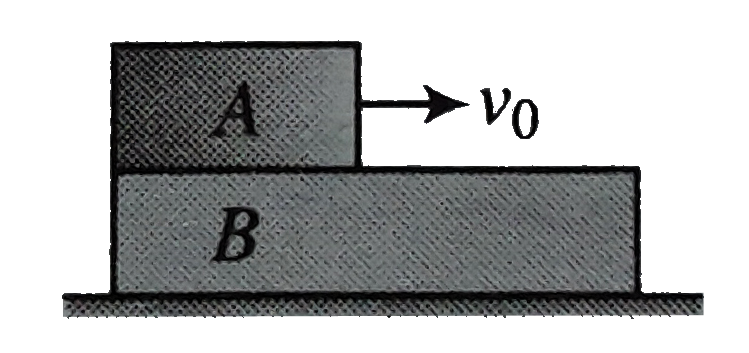
View Solution

