Assuming that earth and mars move in circular orbits around the sun, with the martian orbit being 1.52 times the orbital radius of the earth. The length of the martian year is days is
(1.52)2/3×365
(1.52)3/2×365
(1.52)2×365
(1.52)3×365
The correct Answer is:B
To find the length of the Martian year in days, we can use Kepler's third law of planetary motion. Here's a step-by-step solution:
Step 1: Understand Kepler's Third Law
Kepler's third law states that the square of the orbital period (T) of a planet is directly proportional to the cube of the semi-major axis (a) of its orbit. Mathematically, this is expressed as:
T2∝a3
This can be written as:
T2mT2e=a3ma3e
Where:
- Tm = orbital period of Mars
- Te = orbital period of Earth
- am = orbital radius of Mars
- ae = orbital radius of Earth
Step 2: Define the Known Values
From the problem, we know:
- The orbital radius of Mars is 1.52 times that of Earth:
am=1.52×ae
- The orbital period of Earth is:
Te=365 days
Step 3: Substitute the Known Values into Kepler's Law
Using the relationship between the orbital radii, we can substitute am into Kepler's law:
T2mT2e=(1.52⋅ae)3a3e
This simplifies to:
T2mT2e=(1.52)3
Step 4: Solve for Tm
Now, we can express Tm in terms of Te:
T2m=(1.52)3⋅T2e
Taking the square root of both sides gives us:
Tm=Te⋅(1.52)3/2
Step 5: Substitute Te to Find Tm
Now, substituting Te=365 days:
Tm=365⋅(1.52)3/2
Step 6: Calculate (1.52)3/2
First, calculate (1.52)3/2:
1. Calculate 1.523:
1.523≈3.51
2. Calculate (1.52)3/2:
(1.52)3/2≈√3.51≈1.87
Step 7: Final Calculation
Now, substitute back into the equation for Tm:
Tm≈365⋅1.87≈683.55 days
Conclusion
Thus, the length of the Martian year is approximately 684 days.
---
Kepler's third law states that the square of the orbital period (T) of a planet is directly proportional to the cube of the semi-major axis (a) of its orbit. Mathematically, this is expressed as:
- Tm = orbital period of Mars
- Te = orbital period of Earth
- am = orbital radius of Mars
- ae = orbital radius of Earth
From the problem, we know:
- The orbital radius of Mars is 1.52 times that of Earth:
am=1.52×ae
- The orbital period of Earth is:
Te=365 days
Using the relationship between the orbital radii, we can substitute am into Kepler's law:
Now, we can express Tm in terms of Te:
Now, substituting Te=365 days:
First, calculate (1.52)3/2:
1.523≈3.51
(1.52)3/2≈√3.51≈1.87
Now, substitute back into the equation for Tm:
Thus, the length of the Martian year is approximately 684 days.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Universal law of Gravitations14videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - The Gravitational constant8videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason10videos
KINETIC THEORY
Similar Questions
The planet Mars has two moons. Phobos and Delmos (i) phobos has period 7 hours, 39 minutes and an orbital radius of 9.4×103km. Calculate the mass of Mars. (ii) Assume that Earth and mars move in a circular orbit around the sun, with the martian orbit being 1.52 times the orbital radius of the Earth. What is the length of the martian year in days? (G=6.67×10−11Nm2kg−2)
View SolutionEarth completes one orbit around the sun is
View Solution
Knowledge Check
- Question 1 - Select One
For a satellite moving in a circular orbit around the earth, the ratio of its potential energy to kinetic energy is
A1B−1C2D−2 - Question 2 - Select One
An artificial satellite moving in a circular orbit around the earth has a total energy E0. Its potential energy is
A−E0BE0C2E0D−2E0
Assume that Earth is in circular orbit around the Sun with kinetic energy K and potential energy U, taken to be zero for infinite separation. Then, the relationship between K and U:
View SolutionA satellite of Sun is in a circular orbit around the Sun, midway between the Suna and earth. Find the period of this satellite.
View SolutionIn adjoining figure earth goes around the sun in eliptical orbit on which point the orbital speed is maximum :
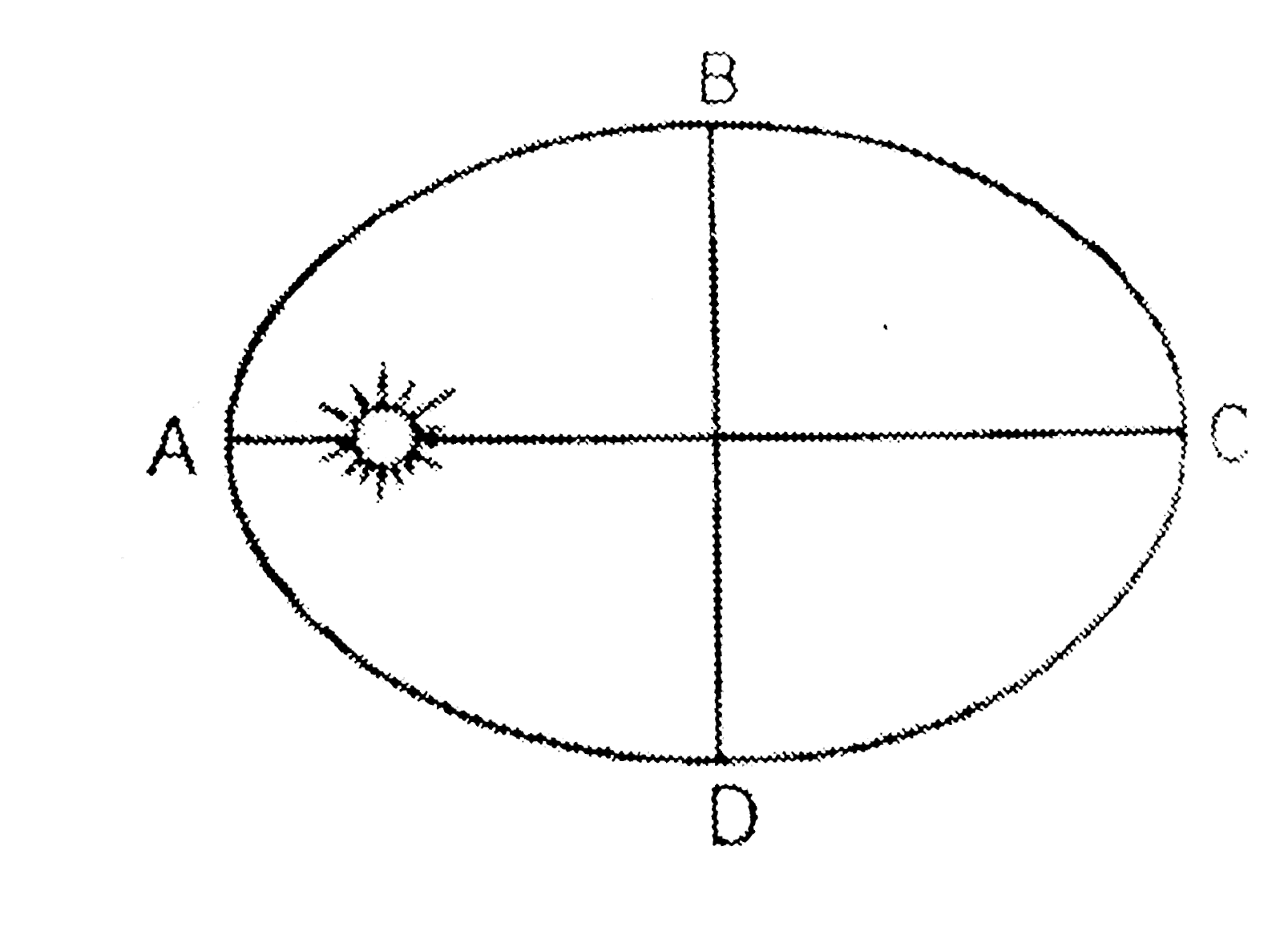 View Solution
View SolutionAn artificial satellite moving in a circular orbit around the earth has a total energy E0. Its potential energy is
View SolutionFor a satellite moving in a circular orbit around the earth, the ratio of its total mechanical energy to kinetic energy
View SolutionTwo identical satellites are orbiting are orbiting at distances R and 7R from the surface of the earth, R being the radius of the earth. The ratio of their
View Solution
