अन्तराल (−π2,π2) में स्थित θ के उन मानो की संख्या जिनके लिए θ≠nπ5,n=0±1,±2तथा tanθ=cot5θ एवं sin2θ=cos4θ है।
The correct Answer is:3
Step by step video, text & image solution for अन्तराल (-(pi)/(2) ,(pi)/(2)) में स्थित theta के उन मानो की संख्या जिनके लिए theta ne (n pi)/( 5 ) , n =0 +- 1,+-2तथा tan theta = cot 5 theta एवं sin 2theta = cos 4theta है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Exercise
134 Videos
- गणितीय तर्कशास्त्रBOOK - ERRORLESS HINDICHAPTER - गणितीय तर्कशास्त्रEXERCISE - Jee Advanced (Reasoning )
3 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
Similar Questions
यदिsin2θ=cosθ,0<θ<π तो θ के संभव मान है।
View Solutionकथन - 1 : ~ (p ↔ ~ q) और p ↔ q तुल्यमान (equivalent) हैं।
कथन -2: ~ (p↔ ~q) एक पुनरुक्ति (tautology) है ।
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
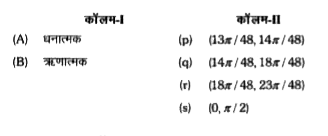
View Solutionsin ((pi) / (2) + theta) * cos ((3 pi) / (2) + theta) * tan ((5 pi) / (2) + theta) * cot ((7 pi) / (2) ) + theta)
View SolutionThe number of values of theta in the interval [-(pi)/(2),(pi)/(2)] and theta!=(n pi)/(5) is where n=0,+-1,+-2 and tan theta=cot(5 theta) and sin(2 theta)=cos(4 theta) is
View SolutionThe number of solutions of tan(5 pi cos theta)=cot(5 pi sin theta) for theta in[0,pi]
View Solutionअंतराल (−π2,π2)में स्थित θ के उन मानों की संख्या जिनके लिये θ≠nπ5,n=0,±1,±2,तथा tan theta = cot 5 theta "एवं " sin 2 theta = cos 4 theta है -
View Solutionयदि (If)=cotθ=sin2θ,0<θ≤90∘(θ≠nπ) तो θ=
View SolutionThe number of values of θ in the interval (−π2,π2) such that θ≠nπ5 for n=0,±1,±2 and tanθ=cot5θ as well as sin2θ=cos4θ, is
View SolutionI : If sin(π4cotθ)=cos(π4tanθ) then θ=nπ+π/4,n∈Z
II : If tan(π2sinθ)=cot(π2cosθ) then sin(θ+π4)=±1√2
View Solutionअन्तराल (−π2,π2) में स्थित θ के उन मानो की संख्या जिनके लिए θ≠nπ5,n=0±1,±2तथा tanθ=cot5θ एवं sin2θ=cos4θ है।
View SolutionThe number of values of θ in the interval [−π2,π2] and θ≠nπ5 is where n=0,±1,±2 and tanθ=cot(5θ) and sin(2θ)=cos(4θ) is
View SolutionS1 : If tanpθ=cotqθ then θ=(2n+1)πp(P+q),n∈Z
S2 : If tan(πsinθ)=cot(πcosθ), then sin(θ+π4)=±12√2
View SolutionThe number of values of θ in the interval (−π2,π2) such that θ≠nπ5for n=0,±1,±2andtanθ=cot5θ as well as sin2θ=cos4θ is
View Solutionअन्तराल (−π2,π2) में θ के उन मानों की संख्या, जिनके लिये θ≠nπ5 जहाँ n=0,±1,±2 तथा tanθ=cot5θ तथा sin2θ=cos4θ है, कितनी होगी
View Solution
