K के निम्न पूर्णाक मानो की संख्या जिसके लिये समीकरण 7cos x + 5 sin x = 2k=1 का एक हल होगा।
4
8
10
12
The correct Answer is:C
Step by step video, text & image solution for K के निम्न पूर्णाक मानो की संख्या जिसके लिये समीकरण 7cos x + 5 sin x = 2k=1 का एक हल होगा। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - JEE Advanced
47 Videos
- त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Solved Multiple Choice Question (ऊँचाई एवं दूरी)
35 Videos
- गणितीय तर्कशास्त्रBOOK - ERRORLESS HINDICHAPTER - गणितीय तर्कशास्त्रEXERCISE - Jee Advanced (Reasoning )
3 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
Similar Questions
0<θ<π2 के लिए 6Σm=1cosec(θ+(m−1)π4)cosec(θ+mπ4)=4√2 का के हल निम्न है।
View Solutionभूमि के एक बिन्दु पर एक मीनार के शिखर का उन्त्रयन कोण 30∘ है यदि मीनार की और 20 मीटर चलने पर उन्यन कोण 60∘ हो जाता है तो मीनार की ऊँचाई हैं
View Solutionकथन - 1 : ~ (p ↔ ~ q) और p ↔ q तुल्यमान (equivalent) हैं।
कथन -2: ~ (p↔ ~q) एक पुनरुक्ति (tautology) है ।
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
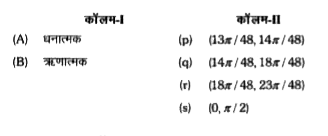
View Solutionरैखिक समीकरण के एक युग्म का हल || दो चर वाले रैखिक समीकरण युग्म का ज्यामितीय अर्थ ||उदाहरण
View Solutionλ के किस मान के लिए निम्न समीकरण के निकाय
2x−y−2z=2,x−2y+z=−4,x+y+λz=4 का कोई हल नहीं है
View Solutionसमीकरण का नियम जिसके लिए α की वास्तविक मानो की संख्या x+3y+5z=αx,5x+y+3z=αy,3x+5y+z=αz के अनंत हल है-
View Solutionनिकाय (k+1)x+8y=4k,kx+(k+3)y=3k−1 के अनंत हलो के लिए k के मानो की संख्या होगी-
View Solutionk के कितने मानो के लिए समीकरण निकाय
(k+1)x+8y=4k
kx+(k+3)y=3k−1
के अनंत हल होंगे ?
View Solutionअवकल समीकरण xdydx+2y=x2(x≠0) का हल जिसके लिए y(1) = 1 है, है
View Solutionदिखाइए कि समीकरण esinx−e−sinx−4=0 का कोई वास्तविक हल नहीं होगा।
View Solutionk का वह मान जिसके लिए समीकरण x2−(3k−1)x+2k2+2k−11=0 के मूल समान होगा, है।
View Solutionअवकलन समीकरण dydx=sin(10x+6y) का हल होगा
View Solutionरैखिक समीकरण के एक युग्म का हल | दो चर वाले रैखिक समीकरण युग्म का ज्यामितीय अर्थ |उदाहरण
View Solutionx अक्ष के समान्तर समतल का समीकरण होगा -
View Solutionयदि x एक वास्तविक संख्या है तो |x|<4 का हल होगा-
View Solution
