कथन-I : समीकरण x34−sinπx+23=0 का [-2, 2] में कम से कम एक हल होगा। क्योंकि
कथन-II : यदि f:[a,b]→R एक फलन है तथा माना c एक संख्या इस प्रकार है कि f(a)<c<f(b) , तब कम से कम एक संख्या n∈(a,b) इस प्रकार है कि f(n) = c है।
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है,कथन-II सत्य है: कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
कथन - I सत्य है परन्तु कथन - II असत्य है।
कथन - I असत्य है परन्तु कथन - II सत्य है।
The correct Answer is:C
Step by step video, text & image solution for कथन-I : समीकरण x^(3)/4 - sin pix +2/3 =0 का [-2, 2] में कम से कम एक हल होगा। क्योंकि कथन-II : यदि f: [a,b] to R एक फलन है तथा माना c एक संख्या इस प्रकार है कि f(a) lt c lt f(b) , तब कम से कम एक संख्या n in (a,b) इस प्रकार है कि f(n) = c है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY Book:ALLEN HINDIChapter:CONTINUITY Exercise:EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न (Comprehension Based Questions)) गद्यांश # 1
Explore 3 Videos
- CONTINUITY Book:ALLEN HINDIChapter:CONTINUITY Exercise:EXERCISE -04 [A] CONCEPTUAL SUBJECTIVE EXERCISE)
Explore 10 Videos
- CONTINUITY Book:ALLEN HINDIChapter:CONTINUITY Exercise:EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) (स्तम्भ सुमेलन (Match the column))
Explore 1 Video
- COMPLEX NUMBERBook:ALLEN HINDIChapter:COMPLEX NUMBERExercise:EXERCISE 5 (B) JEE (ADVANCED) : PREVIOUS YEAR QUESTIONS
Explore 36 Videos
- DEFINITE INTEGRATIONBook:ALLEN HINDIChapter:DEFINITE INTEGRATIONExercise:Exercise - 05 B
Explore 38 Videos
Similar Questions
यदि Sn(x)=xx+1+x2(x+1)(x2+1)+....+x2n(x+1)(x2+1)...(x2n+1) तथा x>1,limn→∞Sn(x)=l
g(x)={√ax+b−1xx≠01x=0
h:R→R,h(x)=x9−6x8−2x7+12x6+x4−7x3+6x2+x−7
यदि g(x),x=0 पर संतत् है, तो a+b बराबर है-
View Solutionयदि f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩−x2जबx≤05x−4जबx<x≤14x2−3xजब1<x<23x+4जबx≥2 f(x) की R में संतता की जांच कीजिए|
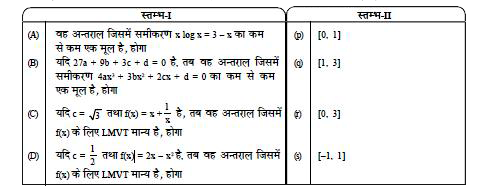
View Solutionनिम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
View Solutionयदि z1,z2,z3 सम्मिश्र संख्याएँ इस प्रकार है कि |z1|=|z2|=|z3|=∣∣∣1z1+1z2+1z3∣∣∣=1, तब |z1+z2+z3| है:
View Solutionसिद्ध कीजिए कि ∫e2e−1∣∣∣logexx∣∣∣dx=52
View Solutionसम्बन्ध R={(x,x3):x,10से कम एक अभाज्य संख्या है} को रोस्टर रूप में लिखिए ।
View Solutionयदि कोई बड़ी संख्या अपने आधे से कम अभाज्य संख्या से भाज्य नही है, तब संख्या कैसी होगी ?
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionएक पासे को 6 बार उछाला गया है। यदि 'पासे पर विषम संख्या प्राप्त होना' एक सफलता है तो निमंलिखित कि प्रायिकताएन क्या होंगी?
(i) तथ्यत: 5 सफलताएँ
(ii) कम से कम 5 सफलताएँ
(iii) अधिकतम 5 सफलताएँ।
View Solutionएक व्यक्ति के लक्ष्य भेदन की प्रायिकता 1/4 है। वह कम से कम कितनी बार गोली चलाये कि लक्ष्य को कम से कम एक बार भेदने की प्रायिकता 2/3 से अधिक हो?
View Solutionएक व्यक्ति एक न्याय सिक्के को कितनी बार उछाले कि कम - से - कम एक चित आने कि प्रायिकता 90 % से अधिक हो ?
View Solutionएक व्यक्ति के लक्ष्य भेदन की प्रायिकता 14 है। यह कम - से - कम कितनी बार गोली चलाए की लक्ष्य को कम से कम एक बार भेदने की प्रायिकता 23 से अधिक हो ?
View Solutionएक सत्य - असत्य प्रकार के 20 प्रश्नो वाली परीक्षा में माना एक विद्यार्थी एक न्याय्य एक सिक्के को उछालकर प्रश्न का उत्तर निर्धारित करता है। यदि पासे पर चित प्रकट हो , तो ' असत्य ' लिखता है। प्रायिकता ज्ञात कीजिए कि वह कम से कम 12 प्रश्नो का सही उत्तर देता है।
View Solutionयदि एक सममित आव्यूह A तथा एक विषम सममित आव्यूह B इस प्रकार है कि A+B=[235−1] तो AB बराबर है
View Solutionनिम्न कथन पर विचार कीजिये ''P(n)=n2−n+41 एक अभाज्य संख्या है'' तो इनमे से कौन-सा एक सत्य है?
View Solution

