f(x)=limn→∞11+nsin2xπ,x=1 पर संतत् है।
The correct Answer is:f
Step by step video, text & image solution for f(x) = lim_(n to infty) 1/(1+n sin^(2)xpi), x =1 पर संतत् है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY Book:ALLEN HINDIChapter:CONTINUITY Exercise:EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) (स्तम्भ सुमेलन (Match the column))
Explore 1 Video
- CONTINUITY Book:ALLEN HINDIChapter:CONTINUITY Exercise:EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) (कथन एवं कारण (Assertion & Reason))
Explore 6 Videos
- CONTINUITY Book:ALLEN HINDIChapter:CONTINUITY Exercise:EXERCISE -02 (BRAIN TEASERS) ( सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर हैं)
Explore 14 Videos
- COMPLEX NUMBERBook:ALLEN HINDIChapter:COMPLEX NUMBERExercise:EXERCISE 5 (B) JEE (ADVANCED) : PREVIOUS YEAR QUESTIONS
Explore 36 Videos
- DEFINITE INTEGRATIONBook:ALLEN HINDIChapter:DEFINITE INTEGRATIONExercise:Exercise - 05 B
Explore 38 Videos
Similar Questions
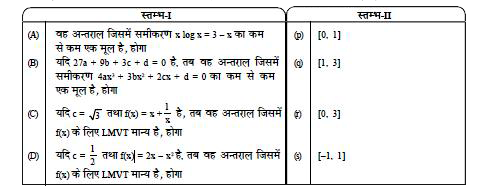
निम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
View Solutionकथन-I : f(x)=sinx+[x],x=0 असंतत् है। क्योंकि
कथन-II: यदि x=a पर g(x) संतत् तथा h(x) असंतत् है, तब g(x)+h(x),x=a पर आवश्यक रूप से असंतत् होगा।
View Solutionमाना खण्डित परिभाषित फलन f(x)=⎧⎪⎨⎪⎩√−x यदिx<00 यदि0≤x≤4x−4 यदिx>4 है। सही विकल्प चुने जो फलन की संतत्ता को परिभाषित करता हो-
View Solutionयदि z1,z2,z3 सम्मिश्र संख्याएँ इस प्रकार है कि |z1|=|z2|=|z3|=∣∣∣1z1+1z2+1z3∣∣∣=1, तब |z1+z2+z3| है:
View Solutionसिद्ध कीजिए कि ∫e2e−1∣∣∣logexx∣∣∣dx=52
View Solutionf(n)=lim_(x rarr0){(1+(sin x)/(2))(1+(sin x)/(2^(2)))......(1+(sin x)/(2^(n)))}^((1)/(x)) then find lim_(n rarr oo)f(n)
View SolutionDiscus the continuity of the function f(x)=lim_(n rarr oo)((1+sin x)^(n)+In x)/(2+(1+sin x)^(n))
View Solutionf(x)=(lim)n→∞tanπx2+(x+1)ns∈xx2+(x+1)n , find (lim)x→0f(x).
View SolutionIf f(x)=lim_(n rarr oo)(tan pi x^(2)+(x+1)^(n)sin x)/(x^(2)+(x+1)^(n)) then
View SolutionConsider the function f(x)=limn→∞(1+cosx)n+5lnx2+(1+cosx)n, then
View SolutionConsider f(x)=limn→∞xn−sinxnxn+sinxn , for x>0,x≠1, f(1) =0, then
View SolutionFor x∈R−{−1n,n∈N}, define f(x)=limn→∞(xx+1+x(x+1)(2x+1)+x(2x+1)(3x+1)) + ….. + upto n terms
then range of f contains exactly……….. Element(s).
View SolutionIf f(n)=limx→0{(1+sinx2)(1+sinx22)...(1+sinx2n)}1x then find limn→∞f(n).
View Solutionमाना f(x)=limn→∞xn−sinxnxn+sinxn,x>0,x≠1 के लिए f(1)=0 है, तो-
View Solutionx=1 पर फलन f(x)=limn→∞ln(2+x)−x2nsinx1+x2n की सांत्यत की जांच कीजिए|
View Solution

