यदि α,β दो सम्मिश्र इस प्रकार है कि ∣∣∣α−β1−¯¯¯αβ∣∣∣=1 हो तो निम्न में से कौन सा सत्य हो सकता है
|α|=1
|β|=1
α=eiθ,θ∈R
β=eiθ,θ∈R
The correct Answer is:A, B, C, D
Step by step video, text & image solution for यदि alpha, beta दो सम्मिश्र इस प्रकार है कि |(alpha-beta)/(1-bar(alpha)beta)|=1 हो तो निम्न में से कौन सा सत्य हो सकता है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE -3 MISCELLANEOUS TYPE QUESTIONS9videos
COMPLEX NUMBER
- BOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE 4 (A) CONCEPTUAL SUBJECTIVE EXERCISE15videos
COMPLEX NUMBER
- BOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE -01 (सही विकल्प चुनिए)31videos
COMPLEX NUMBER
- BOOK - ALLEN HINDICHAPTER - AREA UNDER THE CURVEEXERCISE - Exercise-05 [B]21videos
AREA UNDER THE CURVE
- BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -05 [B] (JEE-ADVANCED: PREVIOUS YEAR QUESTIONS)2videos
CONTINUITY
Similar Questions
निम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
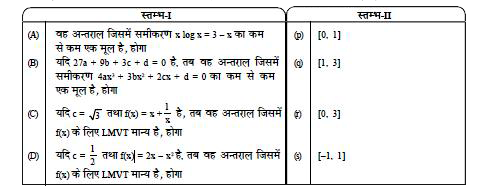
05:00View Solutionसम्मिश्र संख्याओं का मापांक, कोणांक तथा मुख्य कोणांक ज्ञात कीजिएः
a. z=1+cos10π9+isin(10π9)
b. (tan1−i)2
c.z=√5+12i+√5−12i√5+12i−√5−12i02:59View Solution13∑n=1(in+in+1) का मान (जहाँ, i=√−1) क्या हैं?
05:29View Solutionवक्र f(x)=x2+bx−b के बिन्दु (1,1) पर स्पर्श रेखा तथा निर्देशी अक्षो से बना त्रिभुज प्रथम चतुर्थांश में स्थित है | यदि इसका क्षेत्रफल 2 है, तो b का मान है -
03:39View Solutionफलन f(x)=⎧⎨⎩e1/x−1e1/x+1जबx≠01जबx=0 का x=0 पर सततता का परीक्षण कीजिए।
04:35View Solutionयदि α और β भिन्न सम्मिश्र संख्याएँ हैं जहाँ |β|=1, तब ∣∣∣β−α1−¯¯¯αβ∣∣∣ का मान ज्ञात कीजिए ।
02:13View Solutionयदि α और β भिन्न सम्मिश्र संख्याएँ हैं, जहाँ |β|=1, तब ∣∣∣β−α1−¯¯¯αβ∣∣∣ का मान ज्ञात कीजिए।
04:04View Solutionमाना की α,β समीकरण px2+qx+r=0,p≠0 के मूल है | यदि p,q,r समान्तर श्रेणी में हों तथा 1α+1β=4 तो | α−β | का मात्र है :
03:15View Solutionयदि n एक धनात्मक पूर्णांक हो, तो निम्न में से कौन-सा संबंध असत्य है -
06:28View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
03:19View Solutionयदि समीकरण 3x2−6x+5=0 के मूल α,β हो, तो वह समीकरण जिसके मूल α+β व् 2α+β है, होगा
03:46View Solutionयदि α,β समीकरण x2−3x+1=0 के मूल, हो तो वह समीकरण जिसके 1α−2,1β−2 मूल है, होगी।
06:53View Solutionयदि tanα व् tanβ समीकरण x2−px+q=0 के मूल हो, तो sin2(α+β) का मान है
03:41View Solutionयदि ∫e2[1logx−1(logx)2]dx=α+βlog2 हो , तो
02:07View Solutionयदि z एक सम्मिश्र संख्या है, तो निम्न में से कौन-सा कथन सत्य है?
02:00View Solutionयदि समीकरण x2−bxax−c=λ−1λ+1 के मूल α व β इस प्रकार है कि α+β=0 तब λ का मान है
02:21View Solution