∫ex(1+n.xn−1−x2n)(1−xn)1−x2ndx बराबर है-
ex1−xn1+xn+c
ex√1+xn1−xn+c
−ex√1−xn1+xn+c
−ex√1+xn1−xn+c
The correct Answer is:B
Step by step video, text & image solution for inte^(x)((1+n.x^(n-1)-x^(2n)))/((1-x^(n))1-x^(2n))dx बराबर है- by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - INDEFINITE INTEGRATIONEXERCISE - EXERCISE-3 (MISCELLANEOUS TYPE QUESTIONS) (रिक्त स्थानों की पूर्ति कीजिए)4videos
INDEFINITE INTEGRATION
- BOOK - ALLEN HINDICHAPTER - INDEFINITE INTEGRATIONEXERCISE - EXERCISE-3 (MISCELLANEOUS TYPE QUESTIONS) (स्तम्भ सुमेलन)1videos
INDEFINITE INTEGRATION
- BOOK - ALLEN HINDICHAPTER - INDEFINITE INTEGRATIONEXERCISE - EXERCISE-1 CHECK YOUR GRASP (सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर है))4videos
INDEFINITE INTEGRATION
- BOOK - ALLEN HINDICHAPTER - ELLIPSEEXERCISE - EXERCISE - 05 - (B)16videos
ELLIPSE
- BOOK - ALLEN HINDICHAPTER - LIMIT EXERCISE - Do yourself29videos
LIMIT
Similar Questions
सिद्ध कीजिए कि ∫4ex+6e−x9ex−4e−xdx=Ax+Bloge(9x2x−4)+C
02:42View Solutionनिम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
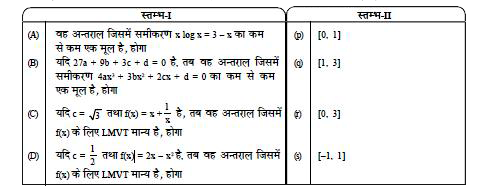
05:26View Solution√1+2tanx(secx+tanx) का x के सापेक्ष पूर्वग है-
03:59View Solutionमाना C1 तथा C2 दो वृत्त हैं, C2,C1 के अन्दर स्थित है। एक वृत्त, C,C1 के अन्दर स्थित है तथा C1 को अन्तः तथा C2 को बाह्य स्पर्श करता है। C के केन्द्र का बिन्दुपथ ज्ञात कीजिए।
01:50View Solutionफलन y = f (x) के आरेख के सापेक्ष निम्न में से कौन से कथन सत्य या असत्य होंगे :
limn→−1+f(x)=1
05:16View SolutionThe coefficient of 1/x in the expansion of (1+x)n(1+1/x)n is n!(n−1)!(n+1)! b. (2n)!(n−1)!(n+1)! c. (2n)!(2n−1)!(2n+1)! d. none of these
02:57View SolutionEvaluate: ∫ex1+nxn−1−x2n(1−xn)√1−x2ndx
06:15View SolutionProve that the coefficients of xn in (1+x)2n is twice the coefficient of xn in (1+x)2n−1.
02:09View Solutionint x ^ (2n-1) cos x ^ (n) dx
View SolutionIf √1−x2n+√1−y2n=an(xn−yn), prove that,
dydx=(xy)n−1.√1−y2n1−x2n07:16View Solution∫xn−1x2n+a2dx=
02:17View Solution√1−x2n+√1−y2n=an(xn−yn) হলে দেখাও যে, dydx=(xy)n−1√1−y2n1−x2n
01:54View Solution∫xn−1x2n+a2dx=
03:16View SolutionShow that
∫[1+nxn−1−x2n(1−xn)√1−x2n]exdx=ex√1+xn1−xn+c04:37View SolutionProve that the coefficients of xn in (1+x)2n is twice the coefficient of xn in (1+x)2n−1.
02:36View Solution