समान मोलरता वाले AICI3(T1) तथा CaCI2(T2) के अति तनु विलयन के क्वथनांक का सही संबन्ध है (T1 तथाT2 क्रमश इनके क्वथनांक है।
T1=T2
T1>T2
T2=T1
T2≥T1
The correct Answer is:2
Step by step video, text & image solution for समान मोलरता वाले AICI_(3) (T_(1)) तथा CaCI_(2) (T_(2)) के अति तनु विलयन के क्वथनांक का सही संबन्ध है (T_(1) तथाT_(2) क्रमश इनके क्वथनांक है। by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- विलयन Book:ALLEN HINDIChapter:विलयन Exercise:Exercise -II (Previous year Questions)
Explore 47 Videos
- विलयन Book:ALLEN HINDIChapter:विलयन Exercise:Exericise -III (Analytical Questions)
Explore 51 Videos
- विलयन Book:ALLEN HINDIChapter:विलयन Exercise:Beginner.s box -4
Explore 4 Videos
- विद्युत रसायन Book:ALLEN HINDIChapter:विद्युत रसायन Exercise:EXERCISE-IV (Assertion & Reason)
Explore 6 Videos
- हाइड्रोकार्बन Book:ALLEN HINDIChapter:हाइड्रोकार्बन Exercise:EXERCISE-IV
Explore 10 Videos
Similar Questions
20 M विलयन के विलेय का घनत्व 1.2gmL−1 है । यदि विलेय का आण्विक द्रव्यमान 100gmol−1 हो तो विलयन की मोललता (molality) है :
View Solutionनिम्न में से किस विलयन की नॉर्मलता सबसे अधिक है।
View SolutionH2Oमें विघुत अपघटय AB2 (सामान्य मोलर द्रव्यमान =164 ) के वियोजन की मात्रा प्रतिशत की गणना कीजिए यदि प्रेक्षित द्रव्यमान 65.6 हो।
View Solution0.1MNH4OH विलयन की मोलर चालकता 0.001MNH4OH विलयन की चालकता से कम होती है
कारण :- तनुता बढ़ाने पर NH4OH विलयन का आयनन बढ़ेगा।
View Solutionकथन :- विकार्बोक्सीलीकरण के लिए क्रियाशीलता का क्रम है
CH3−CH2−COOH>CH3−CH∣CH3−COOH
कारण :- क्रियाशीलता मध्यवर्ती कार्बोकेटायन के स्थायित्व पर निर्भर होती है |
View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View SolutionThe correct relationship between the boiling point of very dilute solutions of AiCI3(t1) and caCI2(t2) having the same molar concentration is:
View SolutionIf an equimolar solution of CaCI_(2) and AICI_(3) in water have boiling point of T_(1) and T_(2) respectively then
View Solutionउस अनुक्रम का प्रथम पाँच पद निकालिए जिसके लिए
t1=1,t2=2 तथा tn+2=tn+tn+1.
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
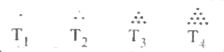
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।
View Solutionआइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View Solution