एक समबाहु त्रिभुज के आधार का समीकरण 2x -y=1 और शीर्ष (-1, 2) है, तब त्रिभुज की भुजा की लम्बाई होगी
√203
2√15
√815
√152
The correct Answer is:A
Step by step video, text & image solution for एक समबाहु त्रिभुज के आधार का समीकरण 2x -y=1 और शीर्ष (-1, 2) है, तब त्रिभुज की भुजा की लम्बाई होगी by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सरल रेखा Book:ERRORLESS HINDIChapter:सरल रेखा Exercise:JEE ADVANCE (More than one correct answer)
Explore 6 Videos
- सरल रेखा Book:ERRORLESS HINDIChapter:सरल रेखा Exercise:JEE ADVANCE (Reasoning type questions)
Explore 4 Videos
- सरल रेखा Book:ERRORLESS HINDIChapter:सरल रेखा Exercise:MULTIPLE CHOICE QUESTIONS (त्रिभुज व चतुर्भुज पर आधारित प्रश्न, बिन्दुपथ )
Explore 19 Videos
- सम्मिश्र संख्यायेंBook:ERRORLESS HINDIChapter:सम्मिश्र संख्यायेंExercise:Jee Advanced (Integer)
Explore 9 Videos
- सारणिक तथा आव्यूह Book:ERRORLESS HINDIChapter:सारणिक तथा आव्यूह Exercise:JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (Matrix Match type questions)
Explore 4 Videos
Similar Questions
बिन्दुओं (1, 3), (5,0) तथा (-1, 2) से निर्मित त्रिभुज के अंदर स्थित सभी बिन्दु निम्न में से कौन से प्रतिबंध संतुष्ट करेंगे
View Solutionरेखा L1: y-x = 0 औरL2 : 2x + y = 0, क्रमशः P और Q पर रेखा L3.::y+ 2 = 0 को प्रतिच्छेद करती है।L1 और L2 के बीच के न्यूनकोण का अर्धक, R पर L3 को प्रतिच्छेद करता है।
कथन - 1 : अनुपात PR:RQ=2√2:√5, क्योंकि
कथन -2 : किसी त्रिभुज में, कोण का अर्धक त्रिभुज को दो समान त्रिभुजों में विभाजित करता है।
View Solutionयदि समद्विबाहु त्रिभुज के आधार के सिरे से शीर्ष (2a,0) व (0,a) है व एक भुजा का समीकरण x=2a है तब त्रिभुज का क्षेत्रफल है
View Solutionमान लीजिए कि z कोई सम्मिश्र संख्या है जिसके लिये |z−3−2i|≤2 सत्य है, तो |2z-6+5i| का न्यूनतम मान है
View Solutionइस खण्ड में कुछ प्रश्न है। प्रत्येक प्रश्न में कॉलम -I में कुछ कथन (A,B, C और D) और कॉलम -II में कुछ कथन (p,q,r,s और t ) है। कॉलम -I का कोई भी कथन कॉलम -II के एक कथन या एक से अधिक कथनो से मेल खाता है। उदाहरण के लिए दिए हुए प्रश्न में यदि कथन B कथनो q और r से मेल खाता है, तो ORS में उस प्रश्न के लिये कथन B के सामने q और r से संबंधित बुलबुलो को काला कीजिए।
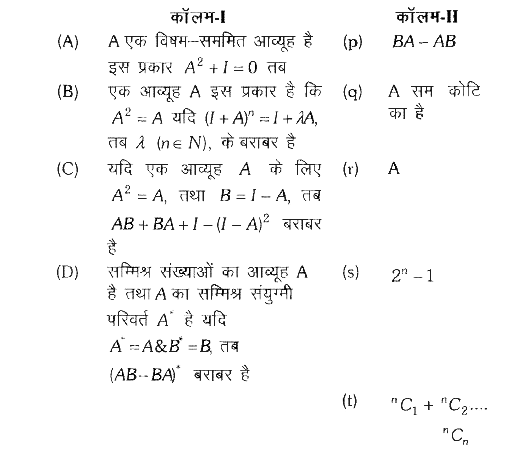
View Solutionसिद्ध कीजिये की बिंदु (a,a),(-a,-a),(-a√3,a√3) एक समबाहु त्रिभुज के निर्देशांक है
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है । यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2)है , तो त्रिभुज की शेष दो भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionत्रिभुज ABC की मध्याकाओं की लम्बाई ज्ञात कीजिए, जिसके शीर्ष A(3, -2), B(0, 6) और C(-2, 4) है ।
View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है। यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2) हो तो त्रिभुज की शेष दो भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionएक परवलय के नाभिलम्ब का समीकरण x+y=8 तथा उसके शीर्ष पर स्पर्शी का समीकरण x+y=12 है, तो उसके नाभिलम्ब की लम्बाई है :
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
View Solution

