Same force acts on two bodies of different masses 3 kg and 5 kg initially at rest. The ratio of time required to acquire same final velocity is
5:3
25:9
9:25
3:5
The correct Answer is:D
To solve the problem of determining the ratio of time required for two bodies of different masses (3 kg and 5 kg) to acquire the same final velocity under the influence of the same force, we can follow these steps:
Step 1: Understand the relationship between force, mass, acceleration, and time.
According to Newton's second law of motion, the force acting on an object is equal to the mass of the object multiplied by its acceleration:
F=m⋅a
Where:
- F is the force,
- m is the mass,
- a is the acceleration.
Step 2: Express acceleration in terms of final velocity and time.
Acceleration can also be defined as the change in velocity over time:
a=v−ut
Since both bodies start from rest, the initial velocity u=0. Therefore, the equation simplifies to:
a=vt
Step 3: Set up the equations for both masses.
For the first body (mass = 3 kg):
F=3⋅a1
Substituting for acceleration:
F=3⋅vt1
Thus:
F=3vt1
(1)
For the second body (mass = 5 kg):
F=5⋅a2
Substituting for acceleration:
F=5⋅vt2
Thus:
F=5vt2
(2)
Step 4: Set the equations equal to each other.
Since the force F is the same for both bodies, we can set equations (1) and (2) equal to each other:
3vt1=5vt2
Step 5: Simplify the equation.
We can cancel v from both sides (assuming v≠0):
3t1=5t2
Step 6: Cross-multiply to find the ratio of times.
Cross-multiplying gives:
3t2=5t1
Step 7: Rearrange to find the ratio t1t2.
Rearranging the equation:
t1t2=35
Conclusion
The ratio of the time required for the two bodies to acquire the same final velocity is:
t1:t2=3:5
According to Newton's second law of motion, the force acting on an object is equal to the mass of the object multiplied by its acceleration:
F=m⋅a
Where:
- F is the force,
- m is the mass,
- a is the acceleration.
Acceleration can also be defined as the change in velocity over time:
a=v−ut
Since both bodies start from rest, the initial velocity u=0. Therefore, the equation simplifies to:
a=vt
For the first body (mass = 3 kg):
F=3⋅a1
Substituting for acceleration:
F=3⋅vt1
Thus:
F=3vt1
(1)
F=5⋅a2
Substituting for acceleration:
F=5⋅vt2
Thus:
F=5vt2
(2)
Since the force F is the same for both bodies, we can set equations (1) and (2) equal to each other:
3vt1=5vt2
We can cancel v from both sides (assuming v≠0):
3t1=5t2
Cross-multiplying gives:
3t2=5t1
Rearranging the equation:
t1t2=35
The ratio of the time required for the two bodies to acquire the same final velocity is:
t1:t2=3:5
Topper's Solved these Questions
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (LAW OF CONSERVATION OF LINEAR MOMENTUM AND ITS APPLICATIONS)
Explore 6 Videos
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (EQUILIBRIUM OF CONCURRENT FORCES)
Explore 7 Videos
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:AIPMT /NEET (MCQ)
Explore 24 Videos
- KINEMATICS Book:MTG GUIDEChapter:KINEMATICS Exercise:AIPMT/ NEET MCQs
Explore 31 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY Book:MTG GUIDEChapter:MOTION OF SYSTEM OF PARTICLES AND RIGID BODY Exercise:AIPMT / NEET (MCQs)
Explore 37 Videos
Similar Questions
Knowledge Check
Two bodies of masses 1 kg and 2 kg moving withy same velocities are stopped by the same force. Then, the ratio of their stopping distances is
A1:2B2:1C√2:1D1:√2At a place where the acceleration due to gravity is 10m sec−2 a force of 5 kg - wt acts on a body of mass 10 kg initially at rest. The velocity of the body after 4 second is
A5m sec−1B10m sec−1C20m sec−1D50m sec−1A force of 5 N acts on a 15 kg body initially at rest. The work done by the force during the first second of motion of the body is
A5 JB56JC6JD75 J
A force of 1000 N is applied on a body of mass 100 kg moving with a velocity of 5m/s. How much time does it require to acquire a velocity of 25m/s ?
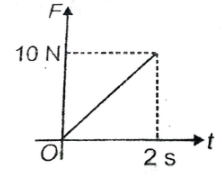
View SolutionA variable force acts on a body of mass 2 kg initially at rest as shown in figure . Calculate the impulse of the force in first 2 seconds and speed of the body after 2 seconds .
View SolutionA force of 5 N acts on a 15 kg body initially at rest. The work done by the force during the first second of motion of the body is
View SolutionA unidirectional force F varying with time t as shown in the figure acts for a short duration 2T on a particle which is initially at rest. Then the velocity acquired by the body is:

View SolutionA force given by the relation F = 8t, acts on a body of mass 2 kg, initially at rest. Find the work done by this force on the body during first 2 seconds of its motion
View Solution

