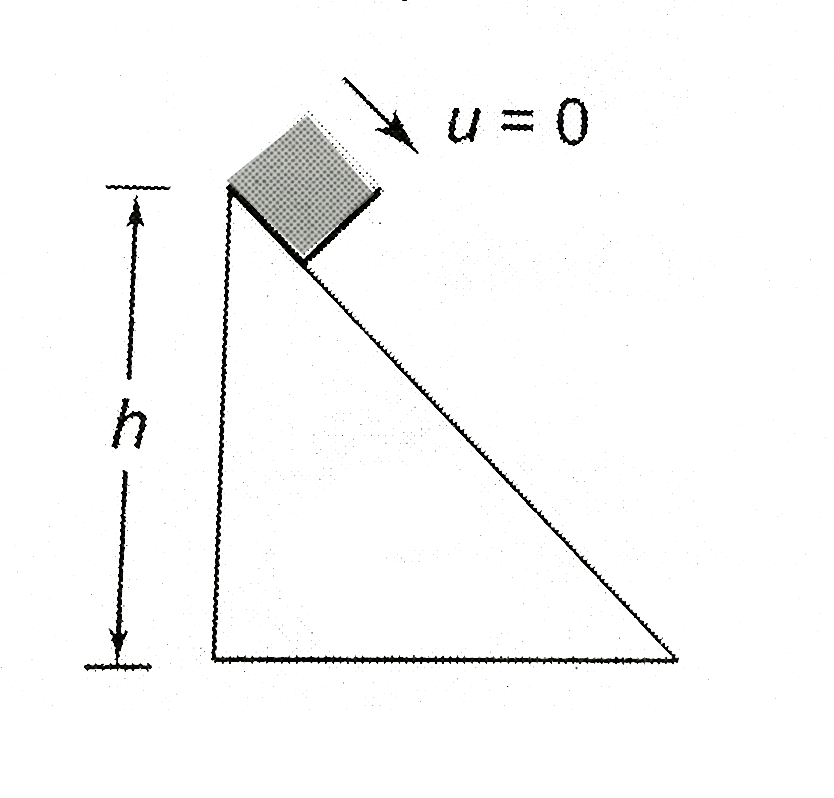A block released from rest from the top of a smooth inclined plane of angle θ1 reaches the bottom in time t1. The same block released from rest from the top of another smooth inclined plane of angle θ2 reaches the bottom in time t2 If the two inclined planes have the same height, the relation between t1andt2 is
t2t1=(sinθ1sinθ2)1/2
t2t1=1
t2t1=sinθ1sinθ2
t2t1=sin2θ1sin2θ2
The correct Answer is:C
Lengths of the two inclined planes are
l1=hsinθ1andl2=hsinθ2
acceleration of the block down the two planes are
a1=gsinθ1anda2=gsinθ2
As l1=12a1t21andl2=12a2t22
∴l1l2=a1t21a2t22ort22t21=a1l2a2l1=gsinθ1gsinθ2×sinθ1sinθ2=sin2θ1sin2θ2
p or t2t1=sinθ1sinθ2
Topper's Solved these Questions
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (LAW OF CONSERVATION OF LINEAR MOMENTUM AND ITS APPLICATIONS)
Explore 6 Videos
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (EQUILIBRIUM OF CONCURRENT FORCES)
Explore 7 Videos
- LAWS OF MOTIONBook:MTG GUIDEChapter:LAWS OF MOTIONExercise:AIPMT /NEET (MCQ)
Explore 24 Videos
- KINEMATICS Book:MTG GUIDEChapter:KINEMATICS Exercise:AIPMT/ NEET MCQs
Explore 31 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY Book:MTG GUIDEChapter:MOTION OF SYSTEM OF PARTICLES AND RIGID BODY Exercise:AIPMT / NEET (MCQs)
Explore 37 Videos
Similar Questions
Knowledge Check
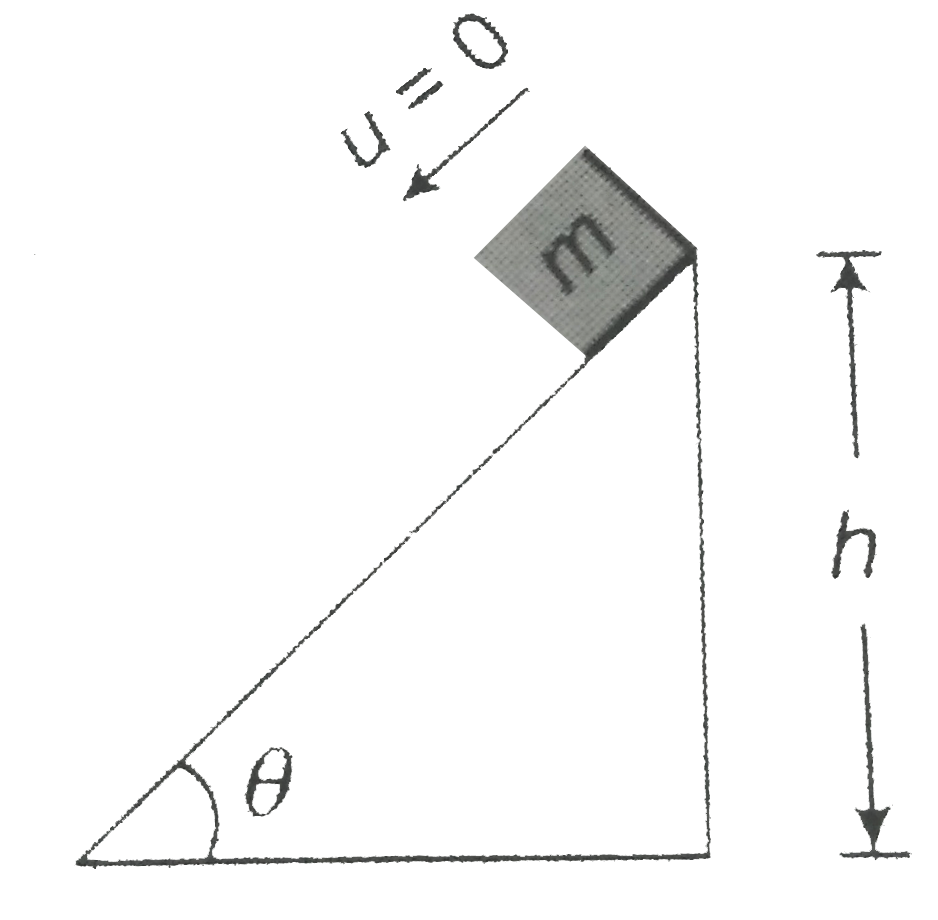
A block released from rest from the top of a smooth inclined plane of angle θ1 reaches the bottom in t1 .
The same block relased from rest from the top of another smooth inclined plane of angle θ2 , reaches the bottom in time t2 . If the two inclined planes have the same height, the relation between t1andt2 isAt2t1=sinθ1(sinθ2)12Bt2t1=1Ct2t1=sinθ1sinθ2Dt2t1=sin2θ1sin2θ2A block released from rest from the top of a smooth inclined plane of angle 30∘ reaches the bottom in time t1. The same block released from rest from the top of another smooth inclined plane of angle 60∘, reaches the bottom in time t2. If the two inclined planes have the same height, the relation between t1 and t2 is
At2t1=12Bt2t1=1Ct2t1=1√3Dt2t1=2A block released from rest from the tope of a smooth inclined plane of angle of inclination θ1=30∘ reaches the bottom in time t1. The same block, released from rest from the top of another smooth inclined plane of angle of inclination θ2=45∘ reaches the bottom in time t2. Time t1 and t2 are related as ( Assume that the initial heights of blocks in the two cases are equal ).
At2t1=1√2Bt2t1=12Ct2t1=1Dt1t2=12
A block is released on an smooth inclined plane of inclination θ. After how much time it reaches to the bottom of the plane?
View SolutionA block is released from top of a smooth inclined plane It reaches the bottom of the plane in √2s The time taken (in second) by the body to cover Ist half of inclined plane is .
View SolutionA block released from rest from the top of a smooth inclined plane of inclination 45∘takes time 't' to reach the bottom . The same block released from rest , from top of a rough inclined plane of same inclination , takes time '2t' to reach the bottom , coefficient of friction is :
View SolutionAn object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
View SolutionA block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
View Solution