Obtain expression for velocities of the two bodies after elastic collision in one dimension .
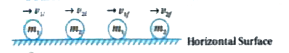Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

Consider elastic collision in one dimension as shown in figure .
Suppose a ball of mass $m_{1}$ moving with velocity $v_{1}$ along X - axis undergoes an elastic collision with a ball of mass $m_{2}$ moving with velocity $v_{2 i} and v_{1 i} > v_{2 i}$
Their final velocities are $v_{1 f} and v_{2 f}$ respectively .
Momentum is conserved in collision .
$∴ m_{1} v_{1 i} + m_{2} v_{2 i} = m_{1} v_{1 f} + m_{2} v_{2 f} ... (1)$
$∴ m_{1} (v_{1 i} - v_{1 f}) = m_{2} (v_{2 f} - v_{2 i})$
Collision is elastic collision so kinetic energy is also conserved .
$\frac{1}{2} m_{1} v_{1 i}^{2} + m_{2} v_{2 i}^{2} = m_{1} v_{1 f}^{2} + m_{2} v_{2 f}^{2} ... . (2)$
$∴ m_{1} (v_{1 i} - v_{1 f}) (v_{1 i} + v_{1 f}) = m_{2} (v_{2 f} - v_{2 i}) (v_{2 f} + v_{2 i})$
From equation (2) ,
$v_{1 i} + v_{1 f} = v_{2 f} + v_{2 i}$
$∴ v_{1 f} = v_{2 f} + v_{2 i} - v_{1 i} ... . (3)$
From equation (1) ,
$m_{1} v_{1 i} + m_{2} v_{2 i} = m_{1} (v_{2 f} + v_{2 i} - v_{1 i}) + m_{2} v_{2 f}$
$∴ m_{1} v_{1 i} + m_{2} v_{2 i} = m_{1} v_{2 f} = m_{1} v_{2 f} + m_{1} v_{2 f} + m_{1} v_{2 i} - m_{1} v_{1} + m_{2} v_{2 f}$
$2 m_{1} v_{1 i} = m_{1} v_{2 i} - m_{2} v_{2 i} - m_{2} v_{2 i} + m_{1} v_{2 f} + m_{2} v_{2 f}$
$2 m_{1} v_{1 i} = (m_{1} - m_{2}) v_{2 i} + (m_{1} + m_{2}) v_{2 f}$
If ball of mass $m_{2}$ having intial velocity
$v_{2 i} = 0$ then
$2 m_{1} v_{1 i} = (m_{1} + m_{2}) v_{2 f}$
$∴ v_{2 f} = \frac{2 m_{1} v_{1 i}}{m_{1} + m_{2}}$
$v_{1 f} = v_{2 f} + v_{2 i} - v_{1 i}$
$= \frac{2 m_{1} v_{1 i}}{m_{1} + m_{2}} - v_{1 i} [∴ v_{2 i} = 0 supposed]$
$= \frac{2 m_{1} v_{1 i} - m_{1} v_{1 i} - m_{2} v_{1 i}}{m_{1} + m_{2}}$
$∴ v_{1 f} = \frac{m_{1} v_{1 i} - m_{2} v_{1 i}}{m_{1} + m_{2}}$
$∴ v_{1 f} = \frac{(m_{1} - m_{2}) v_{1 i}}{(m_{1} + m_{2})}$
In these equations if $m_{1}, m_{2} and v_{1 i}$ is given then the value of $v_{1 f} and v_{2 f}$ can be calculated .

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-WORK, ENERGY AND POWER -QUESTION PAPER (SECTION - D)

Home
Ask Doubt
Profile