Explain work done by a constant force . Solution in Gujrati
Constant force : The magnitude and direction of force acting on the body remains constant during the motion of body , then such type of force is known as constant force .
Definition of work on a trial basis is as under : Work : " The product of magnitude of force and dispalcement during which te force is acts is called work " .
∴Work = Force F × Displacement d ...(1)
where F is the force acting on the body and d is the displacement in the direction of force .
Work is denoted by the dot product of force →F and displacement in the direction of force .
It is not necessary that the displacement of a body is always in the direction of force of force applied .
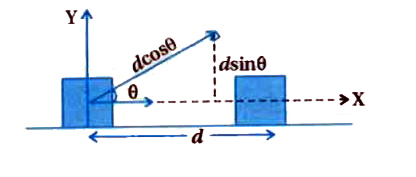
If the displacement →d
It is not necessary that the displacement of a body is always in the dirction of force applied .
If the displacement of body is not in the direction of force applied then the definition of work is given as under by two ways .
(1) Work = Force × Component of displacement in the direction of force
(2) Work = Component of force in the direction of displacement × displacement ...(3)
Understanding these by following figure (a) a body undergoes a displacement →d under the influence of the force →F on the body with θ along the horizontal direction .

Force is not fully responsible for displacement →d for this take the component of force as shown in figure .
(i) The component of force in the horizontal ( displacement →d is not ) direction is Fcosθ
(ii) Perpendicular component fsinθ to the displacement →d is not responsible for horizontal dispalcement .
∴ From the equation (3) of definition of work
W=∣∣→F∣∣cosθ×∣∣→d∣∣
∴W=Fcosθ.d
[∴∣∣→F∣∣=Fand∣∣→d∣∣=d]
The perpendicular components of displacement →d in the direction of force as shown in figure (b) are ,
(1) Component dcosθ in the direction of force →F
(2) Component dsinθ in the perpendicular direction of force →F
∴ From the equation (2) of definition of work ,
W=∣∣→F∣∣×∣∣→d∣∣cosθ
∴W=Fdcosθ ...(5)
[∴∣∣→F∣∣=Fand∣∣→d∣∣=d.∣∣
From equation (4) and (5) , the result obtained by two different definition of work is same .
If θ=00,cos00=1∴ Work in general
W=dcosθ ....(5)
[∴∣∣→F∣∣=Fand∣∣→d∣∣=d]
From equation (4) and (5) , the result obtained by two different definition of work is same .
If θ=00,cos00=1∴ Work in general
W = Fd which is as equation (1) .
The work obtained by the force acting on the body for definite displacement is proportional to the magnitude of force .
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - A Questions - Answers (Try Yourself (VSQs))
74 Videos
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - B Numericals (Numerical From Textual Illustration)
29 Videos
- WAVESBOOK - KUMAR PRAKASHANCHAPTER - WAVESEXERCISE - SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)
23 Videos
Similar Questions
Define the scalar product of two vectors .
View SolutionFind the angle between force →F=(3ˆi+4ˆj−5ˆk) unit and displacement →d=(5ˆi+4ˆj+3ˆk) unit , Also find the projection of F on d .
View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
View SolutionWork Done By A Constant Force
View SolutionExplain what is meant by work. Obtain an expression for work done by a constant force.
View SolutionExplain with graphs the difference between work done by a constant force and by a variable force.
View SolutionExplain the work done by a varible force.
View SolutionExplain with graphs the difference between work done by a constant force and by a variable force.
View SolutionExplain with graphs the difference between work done by a constant force and by a variable force.
View Solutionस्प्रिंग के बल नियतांक द्वारा किया गया कार्य होता है
View SolutionWORK DONE BY A CONSTANT FORCE
View SolutionWork done by a constant force and Work done by a variable force
View SolutionWork done by a constant force and Work done by a variable force
View SolutionWork Done By Constant Force And Examples
View SolutionWork Done By Constant and Variable Forces
View Solution
