Question

Explain the geometrical interpretation of scalar product of two vectors .

Explanation

Suppose the scalar product of two vectros `vec(A) and vec(B)` is given as in the figure (a)
`vec(A) . vec(B) = | hat(A) ||hat(B)| cos theta `
` vec(A) . vec(B) = AB cos theta " "` …(1) which is scalar .

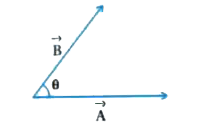
where `theta ` is the angle between `vec(A) and vec(B)`
This product is shown in two ways .
Method 1 :
According to figure (b) , draw a perpendicular from the head of `vec(B) ` on `vec(A)` resulting OM which is shown as in figure OM is the projection of `vec(B)` on to `vec(A)` or it is called the component of `vec(B )` in the direction of `vec(A)` .

` :.` O = component of `vec(B) ` along `vec(A)`
` = B cos theta `
` :. vec(A) . vec(B ) = ABcos theta `
` = A( B cos theta )`
=A(OM) = Magnitude of `vec(A ) xx` component of `vec(A) ` along `vec(A)`
Method 2 :
According to figure (c ) , draw a perpendicular from the head of `vec(A)` on `vec(B)` resulting ON which is shown as in figure ON is the projection of `vec(A)` on a `vec(B )` or it is called component of `vec(A)` in the direction of `vec(B)`

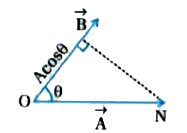
` :. ` ON = component of `vec(A )` along `vec(B)`
` = Acos theta `
` :. vec(A).vec(B) = AB cos theta `
`= B(Acos theta)`
= B(ON)
= Magnitude of `vec(B) xx ` component of `vec(A) ` along `vec(B)`
Hence , the scalar product of two vectors is equal to the product of the magnitude of first vector with the projection of second vector the first vector .