Let $z_{1}$ and $z_{2}$ be two distinct complex numbers and $z = (1 - t) z_{1} + i z_{2}$ , for some real number t with $0 < t < 1$ and $i = \sqrt{- 1}$ . If arg(w) denotes the principal argument of a non-zero compolex number w, then

$| z - z_{1} | + | z - z_{2} | = | z_{1} - z_{2} |$

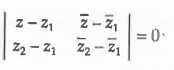
arg|z-z_1| =arg |z-z_2|

ocr_image

arg|z-z_1| =arg |z_2-z_1|

Video Solution

Answer

Step by step video & image solution for Let z_(1) and z_(2) be two distinct complex numbers and z=(1-t)z_(1)+iz_(2), for some real number t with 0 lt t lt 1 and i=sqrt(-1). If arg(w) denotes the principal argument of a non-zero compolex number w, then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS Objective Tests

Topper's Solved these Questions

Knowledge Check

Let $z_{1}$ and $z_{2}$ be two distinct complex numbers and $z = (1 - t) z_{1} + i z_{2}$ , for some real number t with $0 < t < 1$ and $i = \sqrt{- 1}$ . If arg(w) denotes the principal argument of a non-zero compolex number w, then
A $| z - z_{1} | + | z - z_{2} = | z_{1} - z_{2} ∣$
B $a r g (z - z_{1}) = a r g (z - z_{2})$
C $∣ ∣ ∣ \begin{matrix} z - z_{1} & ¯ z - {¯ z}_{1} z_{2} - z_{1} & {¯ z}_{2} - {¯ z}_{1} \end{matrix} ∣ ∣ ∣ = 0$
D $a r g (z - z_{1}) = a r g (z_{2} - z_{1})$
Let $z_{1}, z_{2}$ be two complex numbers such that $z_{1} + z_{2}$ and $z_{1} z_{2}$ both are real, then
A $z_{1} = - z_{2}$
B $z_{1} = {¯ z}_{2}$
C $z_{1} = - {¯ z}_{2}$
D $z_{1} = z_{2}$
Let $z_{1}, z_{2}$ be two complex numbers such that $| z_{1} + z_{2} | = | z_{1} | + | z_{2} |$ . Then,
Aarg $(z_{1}) = arg (z_{2})$
B $arg (z_{1}) + arg (z_{2}) = \frac{π}{2}$
C $| z_{1} | = | z_{2} |$
D $z_{1} z_{2} = 1$

A DAS GUPTA-Objective Tests-Exercise

Home
Ask Doubt
Profile

Let z 1 and z 2 be two distinct complex numbers and z = ( 1 - t ) z 1 + i z 2 , for some real number t with 0 < t < 1 and i = - 1 . If arg(w) denotes the principal argument of a non-zero compolex number w, then

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let z1 and z2 be two distinct complex numbers and z=(1−t)z1+iz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then

Let z1,z2 be two complex numbers such that z1+z2 and z1z2 both are real, then

Let z1,z2 be two complex numbers such that |z1+z2|=|z1|+|z2|. Then,

A DAS GUPTA-Objective Tests-Exercise

Let $z_{1}$ and $z_{2}$ be two distinct complex numbers and $z = (1 - t) z_{1} + i z_{2}$ , for some real number t with $0 < t < 1$ and $i = \sqrt{- 1}$ . If arg(w) denotes the principal argument of a non-zero compolex number w, then

Let $z_{1}$ and $z_{2}$ be two distinct complex numbers and $z = (1 - t) z_{1} + i z_{2}$ , for some real number t with $0 < t < 1$ and $i = \sqrt{- 1}$ . If arg(w) denotes the principal argument of a non-zero compolex number w, then

Let $z_{1}, z_{2}$ be two complex numbers such that $z_{1} + z_{2}$ and $z_{1} z_{2}$ both are real, then

Let $z_{1}, z_{2}$ be two complex numbers such that $| z_{1} + z_{2} | = | z_{1} | + | z_{2} |$ . Then,