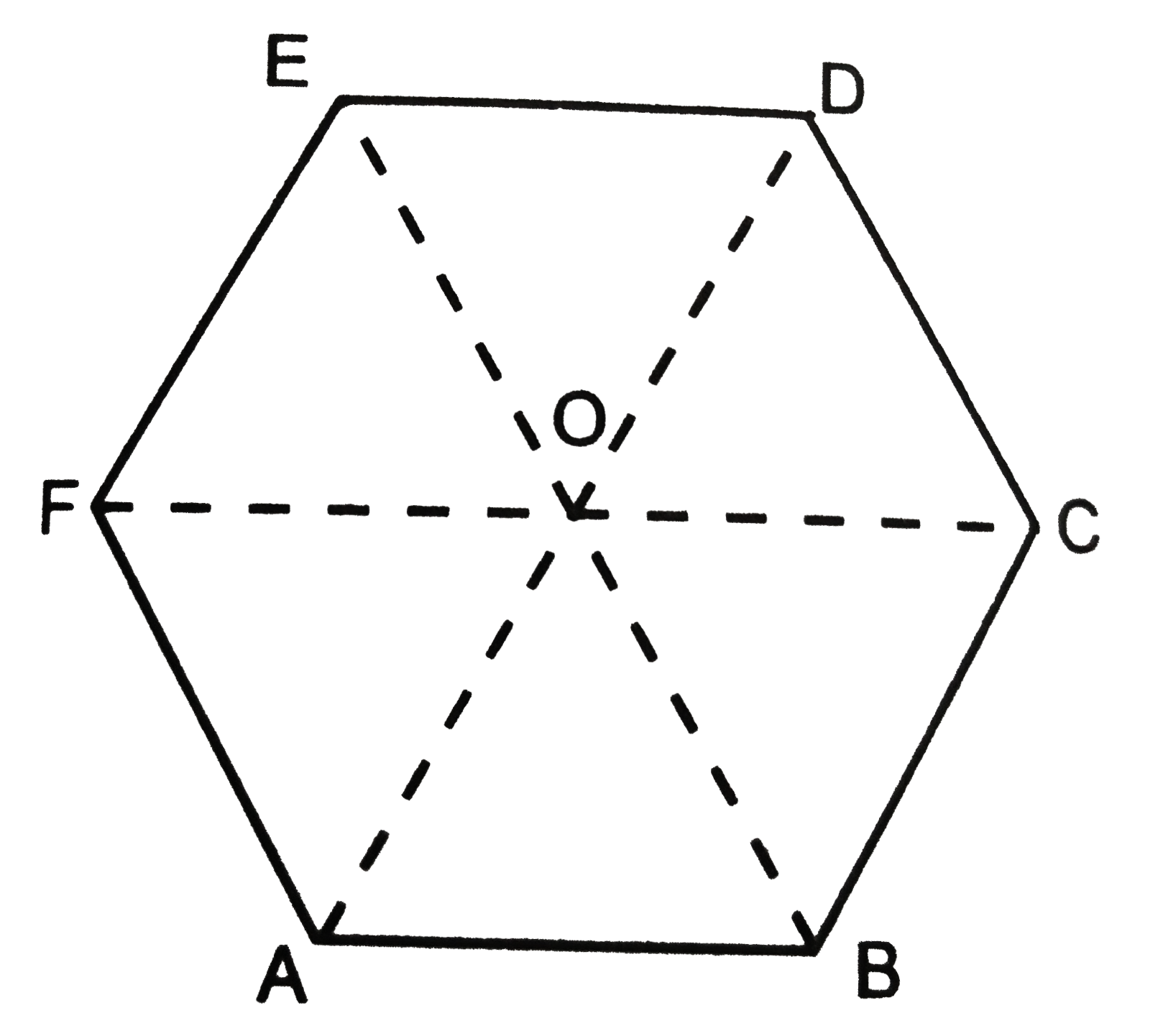
In Fig. ABCDEF is a regular hexagon. Prove that
$- - \to A B + - - \to A C + - - \to A D + - - \to A E + - - \to A F = 6 - - \to A O$ .

Video Solution

Answer

Step by step video & image solution for In Fig. ABCDEF is a regular hexagon. Prove that vec(AB) +vec(AC) +vec(AD) +vec(AE) +vec(AF) = 6 vec(AO). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Vectors and Addition of VectorsBOOK - A DAS GUPTACHAPTER - Vectors and Addition of VectorsEXERCISE - Exercise
16 Videos
Trigonometrical Inequalities and Inequations BOOK - A DAS GUPTACHAPTER - Trigonometrical Inequalities and Inequations EXERCISE - Exercise
19 Videos

Knowledge Check

ABCDEF is a regular hexagon with point O as centre. The value of $- - \to A B + - - \to A C + - - \to A D + - - \to A E + - - \to A F$ is
A $2 - - \to A O$
B $2 - - \to A O$
C $6 - - \to A O$
D0
If ABCDEF is a regular hexagon , then $A \to D + E \to B + F \to C$ equals
A $2 A \to B$
B $\to 0$
C $3 A \to B$
D $4 A \to B$
If ABCDE is a pentagon, then
$- - \to A B + - - \to A E + - - \to B C + - - \to D C + - - \to E D + - - \to A C$ is equal to
A $4 - - \to A C$
B $2 - - \to A C$
C $3 - - \to A C$
D $5 - - \to A C$

A DAS GUPTA-Vectors and Addition of Vectors-Exercise

Home
Ask Doubt
Profile

In Fig. ABCDEF is a regular hexagon. Prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=6−−→AO.

Topper's Solved these Questions

Similar Questions

Knowledge Check

ABCDEF is a regular hexagon with point O as centre. The value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF is

If ABCDEF is a regular hexagon , then A→D+E→B+F→C equals

If ABCDE is a pentagon, then −−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AC is equal to

A DAS GUPTA-Vectors and Addition of Vectors-Exercise

In Fig. ABCDEF is a regular hexagon. Prove that
$- - \to A B + - - \to A C + - - \to A D + - - \to A E + - - \to A F = 6 - - \to A O$ .

ABCDEF is a regular hexagon with point O as centre. The value of $- - \to A B + - - \to A C + - - \to A D + - - \to A E + - - \to A F$ is

If ABCDEF is a regular hexagon , then $A \to D + E \to B + F \to C$ equals

If ABCDE is a pentagon, then
$- - \to A B + - - \to A E + - - \to B C + - - \to D C + - - \to E D + - - \to A C$ is equal to