In a convex polygon the interior angles are in AP, the smallest angle being 120∘ and the common difference 2∘. Find the sum of the sines of the interior angles of the polygon if sin1∘=λ..
To solve the problem step by step, we will follow the logic outlined in the video transcript.
Step 1: Identify the parameters of the arithmetic progression (AP)
We know that the smallest angle of the polygon is 120∘ and the common difference is 2∘.
- Let the first term a=120∘
- Let the common difference d=2∘
Step 2: Determine the maximum angle in the polygon
In a convex polygon, all interior angles must be less than 180∘. Therefore, the largest angle can be calculated as follows:
- The last term of the AP can be expressed as:
Last term=a+(n−1)d
Setting this less than 180∘:
120+(n−1)⋅2<180
(n−1)⋅2<60
n−1<30⇒n<31
Thus, the maximum number of angles n can be 30.
Step 3: Calculate the angles of the polygon
The angles of the polygon are:
120∘,122∘,124∘,…,178∘
This is an arithmetic series with n=30 terms.
Step 4: Find the sum of the sines of the interior angles
We can use the formula for the sum of sines of an arithmetic series:
S=n2⋅(sin(a)+sin(l))
where l is the last term.
In our case:
- l=178∘
- n=30
Step 5: Calculate the sum of the sines
Using the sine addition formula:
S=302⋅(sin(120∘)+sin(178∘))
We know that:
- sin(120∘)=sin(180∘−60∘)=sin(60∘)=√32
- sin(178∘)=sin(180∘−2∘)=sin(2∘)
Thus,
S=15⋅(√32+sin(2∘))
Step 6: Express sin(2∘) in terms of λ
Using the small angle approximation, we can express sin(2∘) as:
sin(2∘)=2sin(1∘)cos(1∘)=2λcos(1∘)
Step 7: Substitute back into the sum
Now substituting back into our sum:
S=15⋅(√32+2λcos(1∘))
Step 8: Final expression
The final expression for the sum of the sines of the interior angles of the polygon is:
S=15√32+30λcos(1∘)
We know that the smallest angle of the polygon is 120∘ and the common difference is 2∘.
- Let the common difference d=2∘
In a convex polygon, all interior angles must be less than 180∘. Therefore, the largest angle can be calculated as follows:
Last term=a+(n−1)d
Setting this less than 180∘:
120+(n−1)⋅2<180
(n−1)⋅2<60
n−1<30⇒n<31
Thus, the maximum number of angles n can be 30.
The angles of the polygon are:
120∘,122∘,124∘,…,178∘
This is an arithmetic series with n=30 terms.
We can use the formula for the sum of sines of an arithmetic series:
S=n2⋅(sin(a)+sin(l))
where l is the last term.
- l=178∘
- n=30
Using the sine addition formula:
S=302⋅(sin(120∘)+sin(178∘))
We know that:
- sin(120∘)=sin(180∘−60∘)=sin(60∘)=√32
- sin(178∘)=sin(180∘−2∘)=sin(2∘)
S=15⋅(√32+sin(2∘))
Using the small angle approximation, we can express sin(2∘) as:
sin(2∘)=2sin(1∘)cos(1∘)=2λcos(1∘)
Now substituting back into our sum:
S=15⋅(√32+2λcos(1∘))
The final expression for the sum of the sines of the interior angles of the polygon is:
S=15√32+30λcos(1∘)
Topper's Solved these Questions
Similar Questions
Knowledge Check
Some of the interior angle of the polygon is
A(n−4)90∘B(2n−4)180∘C(2n−4)90∘D(n−4)180∘Find the sum of the interior angles of the polygon given below .
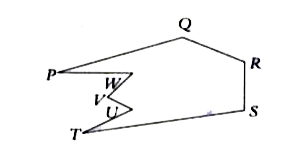 A1080∘B1440∘C1800∘D900∘
A1080∘B1440∘C1800∘D900∘The interior angles of a polygon are in AP. If the smallest angle be 120∘ and the common difference be 5∘, then the number of side is
A8B10C9D6
Find the sum of the interior angles of the polygon gives below.
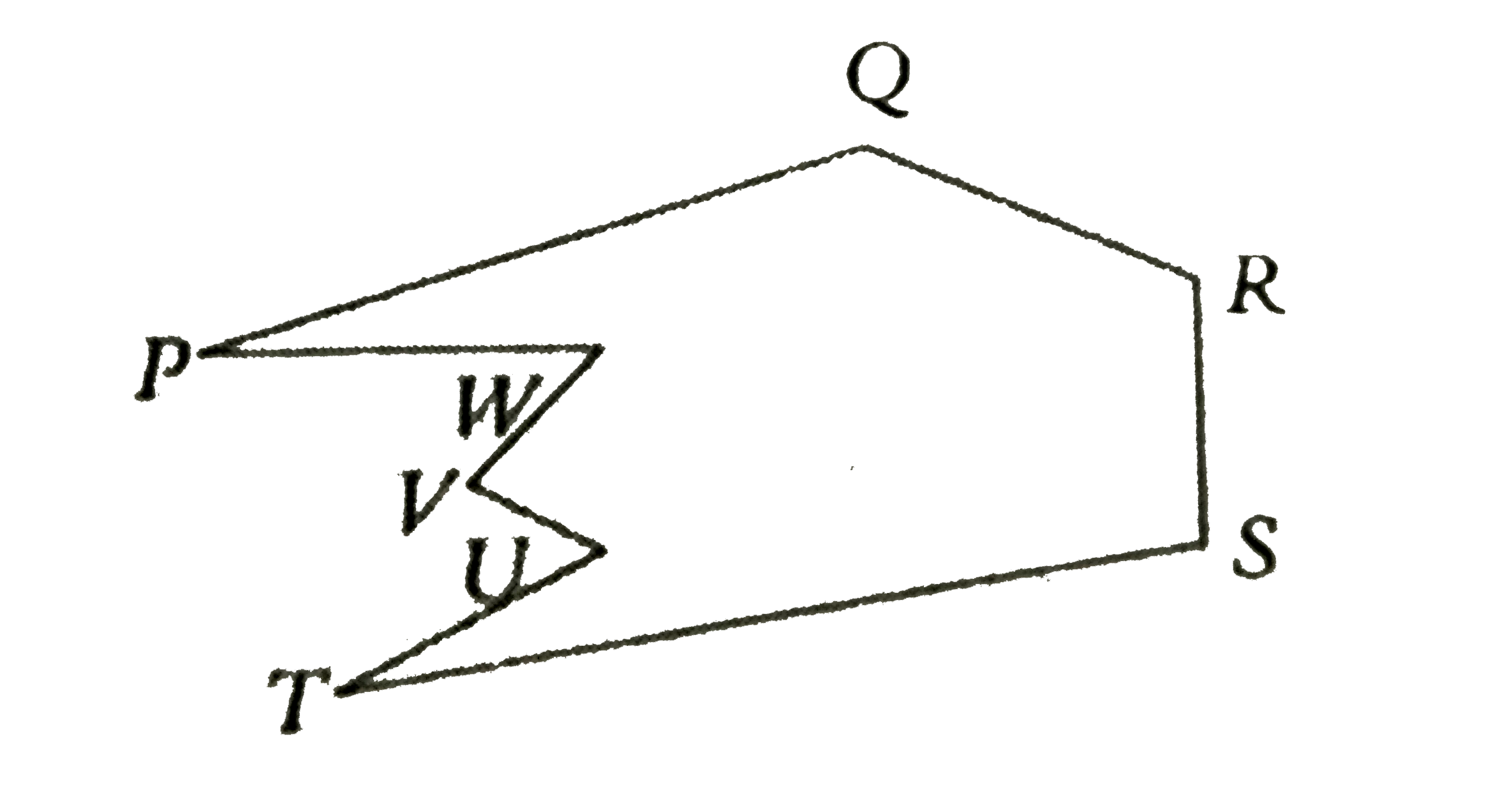
View SolutionFind the sum of the interior angles of a polygon of 8 sides.
View SolutionThe interior angles of a polygon are in A.P. the smallest angle is 120∘ and the common difference is 5∘. Find the number of sides of the polygon.
View SolutionFind the sum of the interior angles of the an 8-sided polygon.
View SolutionThe interior angle of polygon are in A.P., the smallest angle is 750 and the common difference is 100. Find the numberof sieds of the polygon.
View Solution

