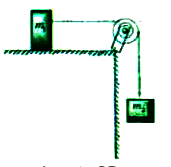
Two blocks asre connected by a string as shown in figure. They are released from rest. Show that after they moved a distance L, their common speed is given by √2(m2−μm1)gL(m1+m2) where μ is the coefficient of friction.
 Solution in Telugu
Solution in Telugu
In moving a distance L by m1andm2 the PE will be lost by m2 only and will be m2gl, while work done by friction will be only on m1 and will be μm1gL. Now as the string is inextensible v1=v2=v and so, the gain in KE wil be = (1/2)(m1+m2)v2. By conservation of energy.
Loss in PE = Grain in KE + WD against friction
i.e., m2gL=12(m1+m2)v2+μm1gL
v=√2(m2−μm1)gL(m1+m2)
Topper's Solved these Questions
- WORK, POWER & ENERGY Book:AAKASH SERIESChapter:WORK, POWER & ENERGY Exercise:EXERCISE - I
Explore 78 Videos
- WORK, POWER & ENERGY Book:AAKASH SERIESChapter:WORK, POWER & ENERGY Exercise:EXERCISE - II (SCALARS (OR) DOT PRODUCT)
Explore 9 Videos
- WORK POWER ENERGYBook:AAKASH SERIESChapter:WORK POWER ENERGYExercise:EXERCISE - 3
Explore 61 Videos
Similar Questions
If l1,m1,n1 and l2,m2,n2 are the direction cosines of two vectors and θ is the angle between them, then the value of cos θ is
View SolutionIf →P=2ˆi+3ˆj−4ˆkand→Q=5ˆi+2ˆj+4ˆk. Find the angle between the two vectors.
View SolutionIf →A+→B=→Rand2→A+→B is perpendicular to →B then
View SolutionTwo block of masses m_(1) and m_(2) are connected as shown in the figure. The acceleration of the block m_(2) is:
View SolutionTwo blocks M_(1) and M_(2) having equal mass are free to move on a horizontal frictionless surface. M_(2) is attached to a massless spring as shown in figure. Initially M_(2) is at rest and M_(1) is moving toward M_(2) with speed upsilon and collides head-on with M_(2) .
View SolutionIn the figure shown m_(1)=5 kg,m_(2) = 10 kg & friction coefficient between m_(1) & m_(2) is mu=0.1 and ground is frictionless then :
View SolutionIn figure-2.86, the blockA of mass M_(1) rests on a rough horizontal surface. The coefficient of friction between the block and the surface is mu . A uniform plank B, of mass M_(2) rests on A. B is prevented from moving by connecting it to a light rod R which is hinged at one end H.The coefficient of friction between A and B is mu . Findthe acceleration of blocks A and C. [(M_(3)g-mug(M_(1)+2M_(2)))/((M_(1)+M_(3)))]
View SolutionTwo blocks m1=4 kg and m2=2 kg connected by a weightless rod on a plane having inclination of 37∘ the coefficient of friction of m1 and m2 with the inclined plane are μ=0.25 each. Then the common accleration of the two blocks and the tension in the rod are

View SolutionIf, in Q.19, coefficient of friction between m1 and the wall is μ,and f1 and f2 are respectively, the force of friction on m1 and m2, then :
View SolutionIn the figure shown if coefficient of friction is mu , then m_(2) will start moving upwards if
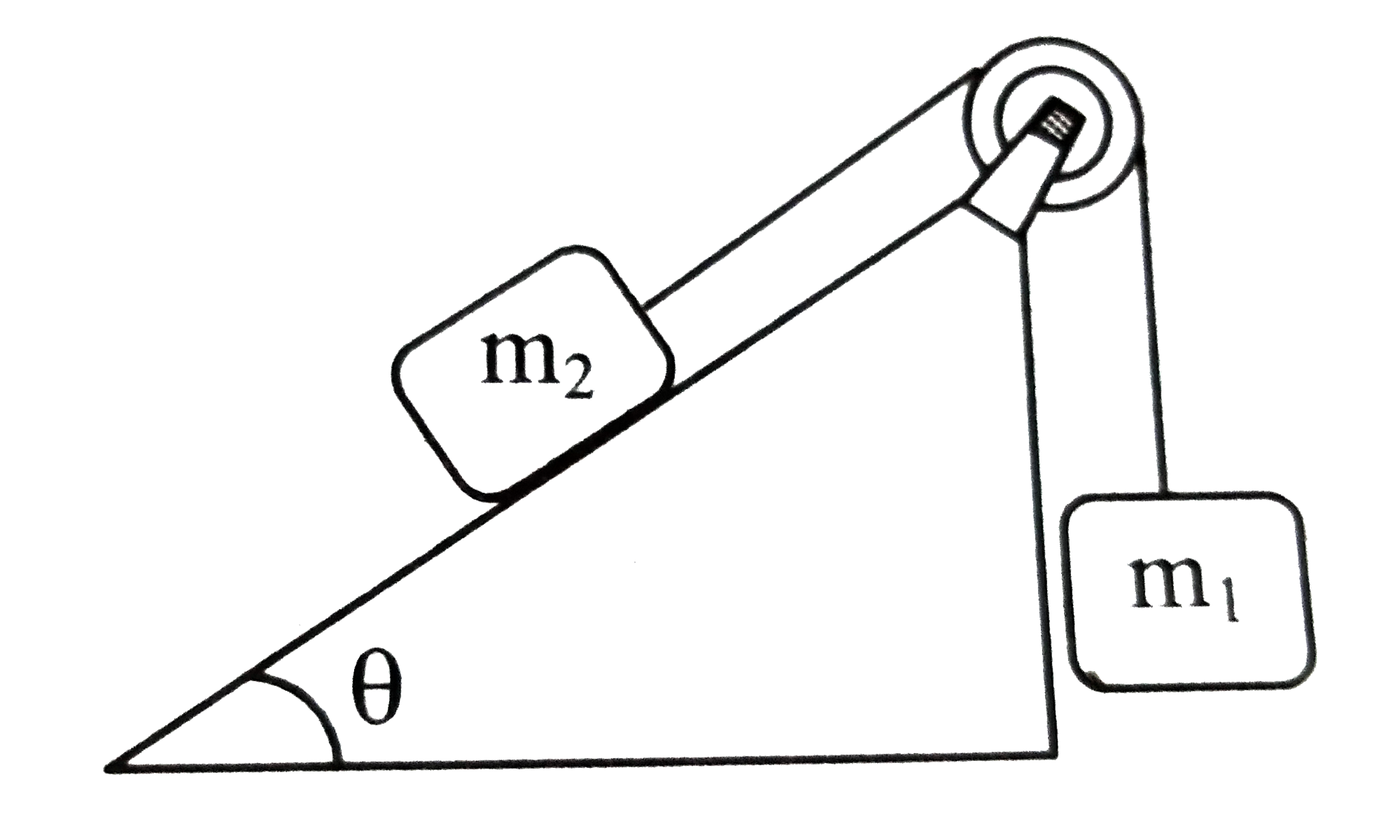
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionTwo blocks M1 and M2 having equal mass are free to move on a horizontal frictionless surface. M2 is attached to a massless spring as shown in figure. Initially M2 is at rest and M1 is moving toward M2 with speed υ and collides head-on with M2.

View SolutionThe masses m1=10 kg m2=5 kg are connected by a ideal string as shown in figure. The coefficient of friction m1 and the surface is μ=0.2.Assuming that the system is released from rest. Calculate the velocity of block when m2 has descended by 4m? [g=10ms−2]
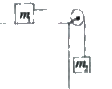
View SolutionTwo blocks asre connected by a string as shown in figure. They are released from rest. Show that after they moved a distance L, their common speed is given by √2(m2−μm1)gL(m1+m2) where μ is the coefficient of friction.

View Solution