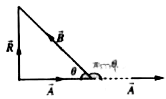
The resultant of two vectors vec(A) and vec(B) is perpendicular to vec

The resultant of two vectors $\to A and \to B$ is perpendicular to the vector $\to A$ and its magnitude is equal to half the magnitude of vector $\to B$ . What is the angle between $\to A and \to B$ ?
A $30^{\circ}$
B $45^{\circ}$
C $150^{\circ}$
D $120^{\circ}$
The resultant of two vectors $\to A$ and $\to B$ is perpendicular to the vector $\to A$ and its magnitudes is equal to half of the magnitudes of vector $\to B$ (figure). The angle between $\to A$ and $\to B$ is

A $120^{\circ}$
B $150^{\circ}$
C $135^{\circ}$
DNone of these
The resultant of $\to A and \to B$ is perpendicular to $\to A$ . What is angle between $\to A and \to B$ ?
A ${cos}^{- 1} (\frac{A}{B})$
B ${cos}^{- 1} (- \frac{A}{B})$
C ${sin}^{- 1} (\frac{A}{B})$
D ${sin}^{- 1} (- \frac{A}{B})$

The resultant of two vectors $\to A$ and $\to B$ is perpendicular to $\to A$ and equal to half of the magnitude of $\to B$ . Find the angle between $\to A$ and $\to B$ ?