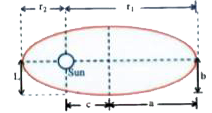
The largest and the shortest distance of the earth from the sun are $r_{1}$ and $r_{2}$ respectively. Calculate the distance from the sun when it is at perpendicular distance to major axis of the orbit drawn from the sun

Text Solution

Verified by Experts

Since $e = \frac{c}{a} \Rightarrow c = e a ∴ r_{1} = a + c = a + e a = a (1 + e)$
$r_{2} = a - c = a - e a = a (1 - e)$
Required distance $L = \frac{b^{2}}{a}$ (semi latus rectum )
we have $r_{1} + r_{2} = 2 a$ and $r_{- r}_2 = a (1 + e) - a (1 - e) = 2 a e \Rightarrow e = \frac{r_{1} - r_{2}}{r_{1} + r_{2}}$
Also $b^{2} = a^{2} (1 - e^{2})$
$∴ L = \frac{b^{2}}{a} = \frac{a^{2} (1 - e^{2})}{a} = a (1 - e^{2})$
$= (\frac{r_{1} + r_{2}}{2}) [1 - {(\frac{r_{1} - r_{2}}{r_{1} + r_{2}})}^{2}]$
on simplification , $L = \frac{2 r_{1} r_{2}}{r_{1} + r_{2}} or \frac{2}{L} = \frac{1}{r_{1}} + \frac{1}{r_{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Similar Questions

Knowledge Check

Question 1 - Select One
The largest and the shortest distance of the earth from the sun are $r_{1}$ and $r_{2}$ . Its distance from the sun when it is at perpendicular to the major -axis of the orbit drawn from the sun is
A $\frac{η + η_{2}}{4}$
B $\frac{η + η_{2}}{η_{1} - η_{2}}$
C $\frac{2 η r_{1} r_{2}}{r_{1} + r_{2}}$
D $\frac{r_{1} + r_{2}}{3}$
Question 2 - Select One
The largest and the shortest distance of the earth from the sun are $r_{1}$ and $r_{2}$ , its distance from the sun when it is at the perpendicular to the major axis of the orbit drawn from the sun
A $\frac{r_{1} + r_{2}}{4}$
B $\frac{r_{1} r_{2}}{r_{1} + r_{2}}$
C $\frac{2 r_{1} r_{2}}{r_{1} + r_{2}}$
D $\frac{r_{1} r_{2}}{3}$
Question 3 - Select One
The distance of the earth from the sun is about
A1500 million km .
B300 million km
C227 million km
D149 million km.

Recommended Questions

Home
Ask Doubt
Profile