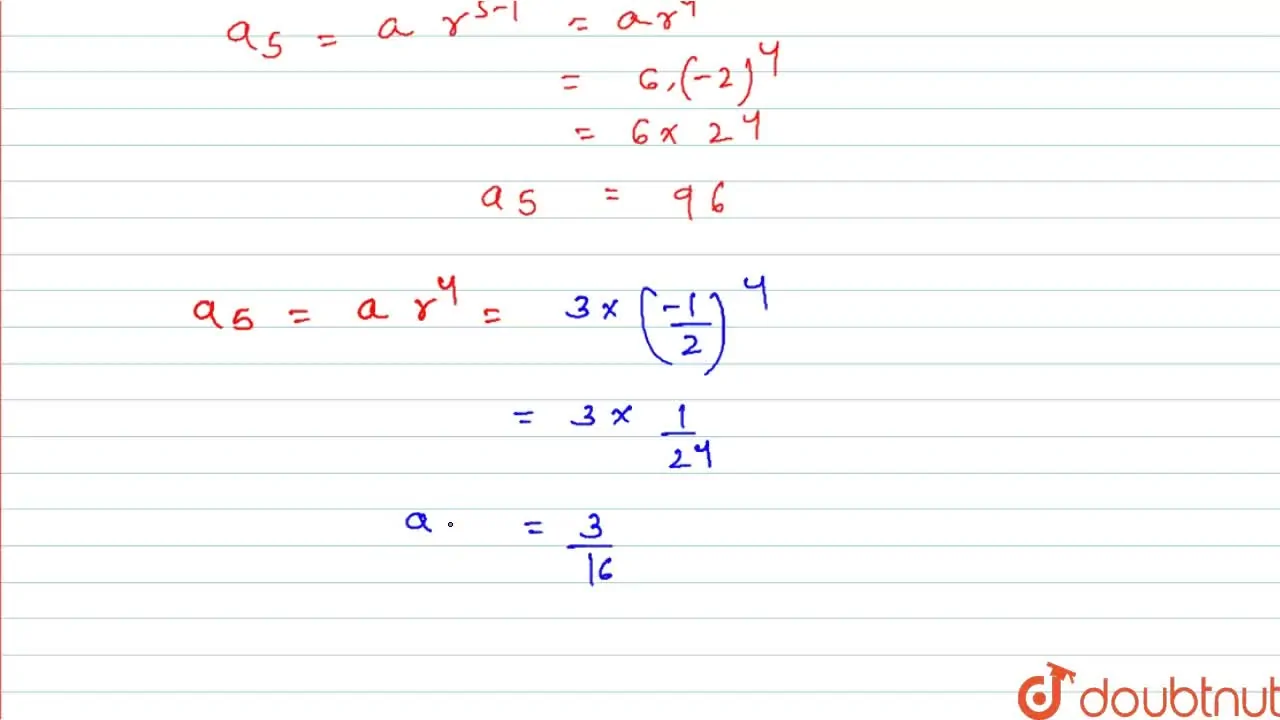Sum of an infinite G.P. is 2 and sum of their cubes is 24, then 5th term of the G.P. is
The correct Answer is:A
Step by step video, text & image solution for Sum of an infinite G.P. is 2 and sum of their cubes is 24, then 5th term of the G.P. is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - PROGRESSIONSEXERCISE - EXERCISES LEVEL-1 (Single Correct Answer Type Questions)65videos
PROGRESSIONS
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - PROGRESSIONSEXERCISE - EXERCISES LEVEL-2 (Single Correct Answer Type Questions)11videos
PROGRESSIONS
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - PROGRESSIONSEXERCISE - SOLVED EXAMPLES LEVEL (Numerical Answer Type Questions)21videos
PROGRESSIONS
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Previous Years B-Architecture Entrance Examination Papers21videos
PROBABILITY
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Questions from previous Years. B - architecture entrance examination papers16videos
QUADRATIC EQUATIONS
Similar Questions
The sum of an infinite numbers of a G.P. is 2 and the sum of their cubes is 24. The second term of the G.P. is
View SolutionThe sum of an infinite G.P. is 57 and the sum of their cubes is 9457, find the G.P.
View SolutionThe sum of an infinite G.P. is 4 and the sum of their cubes is 192. Find the first term :
View Solution. The sum of an infinite number of terms of a G.P. is 20, and the sum of their squares is 100, then the first term of the G.P. is
View SolutionThe sum of an infinite G.P. is 4 and the sum of their cubes is 192. Find the first term :
View SolutionThe sum of an infinite GP is 57 and the sum of their cubes is 9747. Find the GP.
View SolutionThe sum of an infinite G.P. is 5 and the sum of the squares of these terms is 15. Find the G.P.
View SolutionIf the sum of an infinite G.P is 32 and the some of its first two terms is 24, find the series.
View SolutionIf the sum of an infinite G.P. be 3 and the sum of the squares of its term is also 3, then its first term and common ratio are
View SolutionSum of an infinite G.P is 2 and sum of its two terms is 1.If its second terms is negative then which of the following is /are true ?
View Solution