In the given figure, AB and DC are both perpendicular to line segment AD. BC intersects AD at P and P is the midpoint of AD. Prove that, ( 1 ) AB = CD ( 2 ) P is the midpoint of BC.
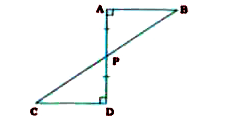
Step by step video & image solution for In the given figure, AB and DC are both perpendicular to line segment AD. BC intersects AD at P and P is the midpoint of AD. Prove that, ( 1 ) AB = CD ( 2 ) P is the midpoint of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:TRIANGLESExercise:MULTIPLE CHOICE QUESTIONS
Explore 15 Videos
- TRIANGLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:TRIANGLESExercise:SUMS TO ENRICH REMEMBER
Explore 9 Videos
- TRIANGLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:TRIANGLESExercise:EXERCISE 7.5
Explore 4 Videos
- SURFACE AREAS AND VOLUMESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SURFACE AREAS AND VOLUMESExercise:MULTIPLE CHOICE QUESTIONS
Explore 18 Videos
Similar Questions
In the given figure, AD and BC are equal perpendicualrs to a line segment AB.
Show that CD bisects AB.
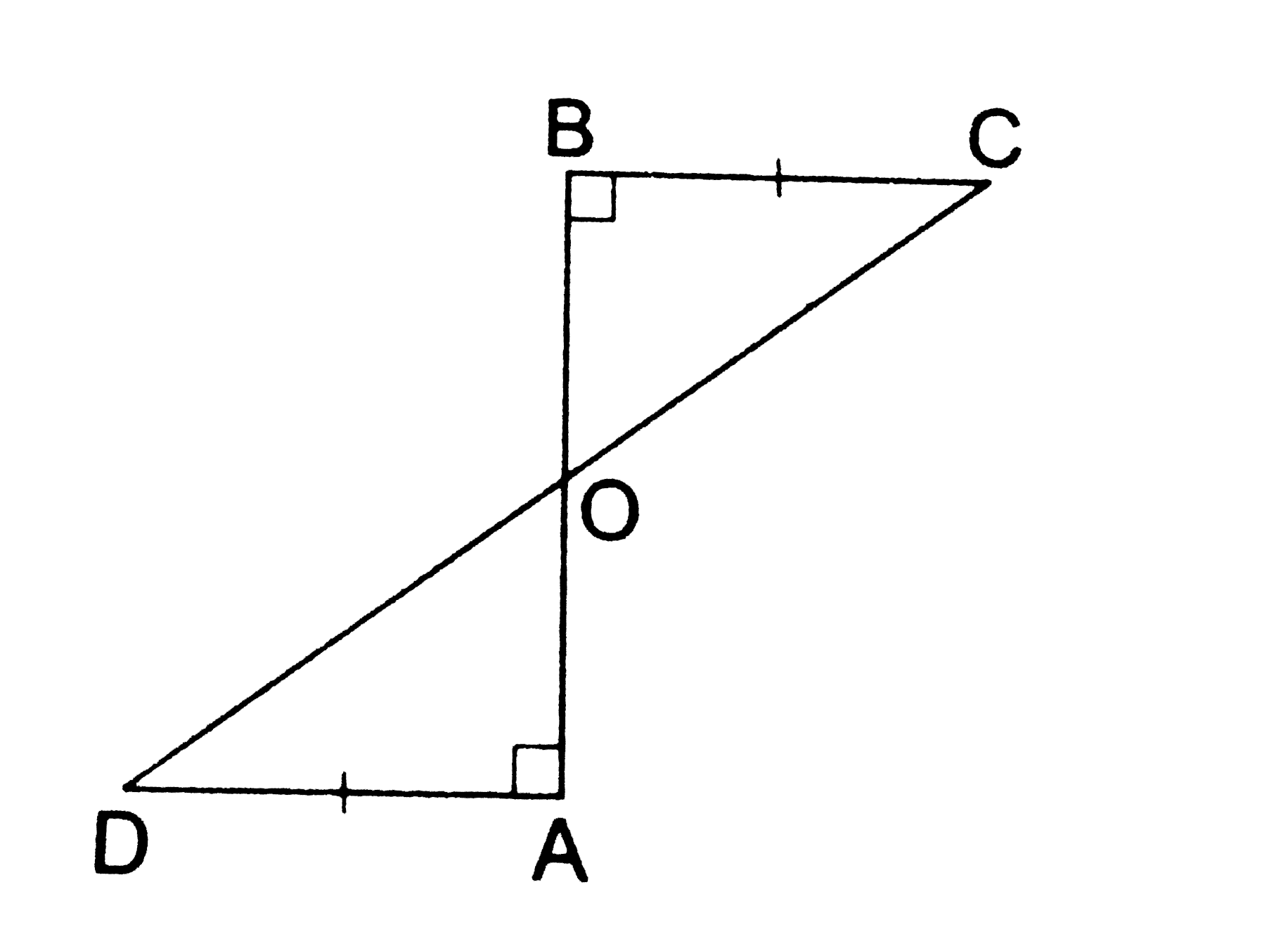
View SolutionAD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
View SolutionAD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
View SolutionIn the given figure, AB||CDandO is the midpoint of AD.
Show that (i) ΔAOB≅ΔDOC.
(ii) O is the midpoint of BC.
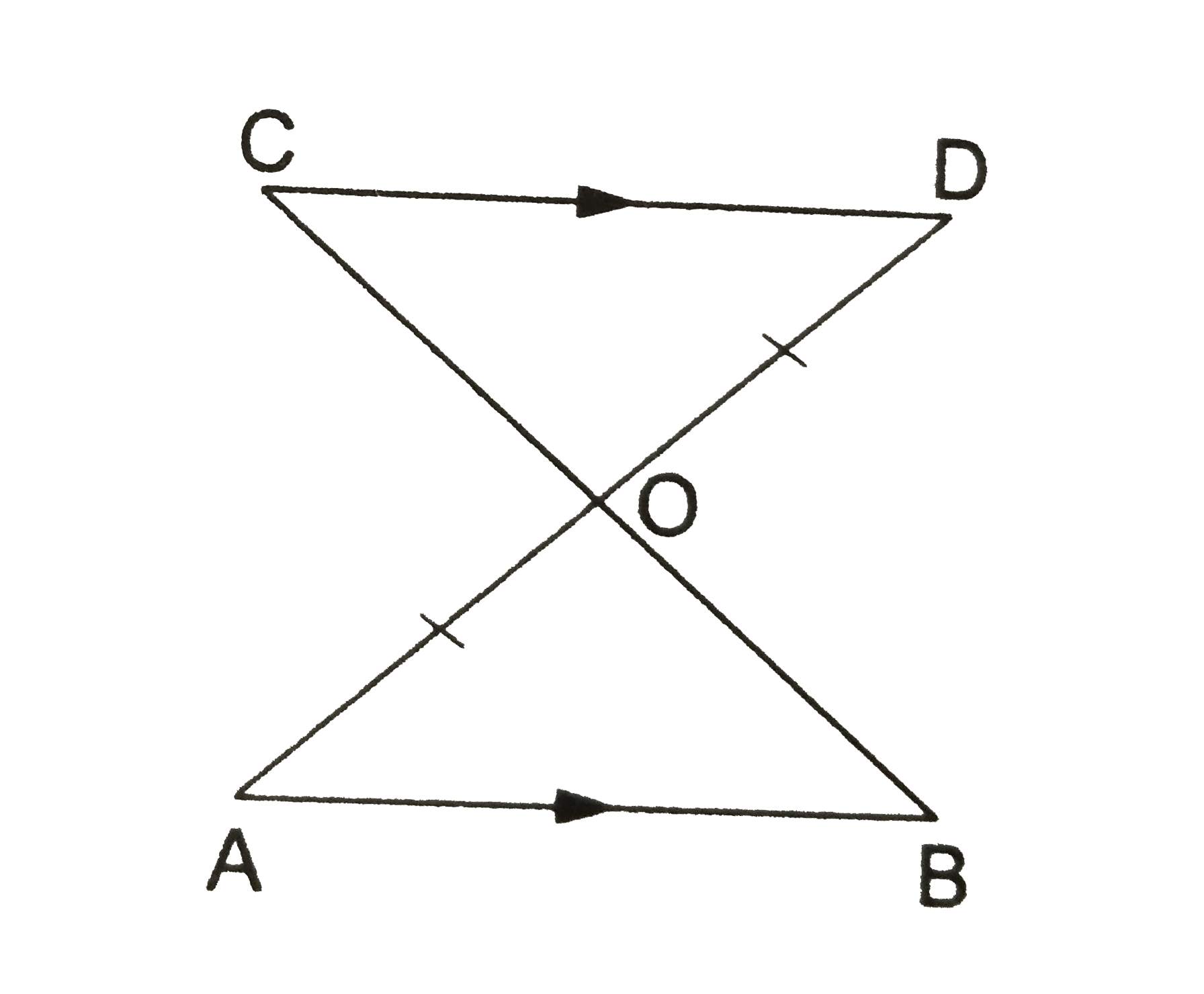
View SolutionIn the given figure. AB∣CDandO is the midpoint of AD.
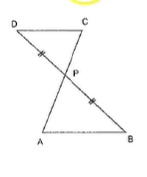
View SolutionIn Figure, if AB∣∣DC and P is the mid-point BD, prove that P is also the midpoint of AC
View SolutionAD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.
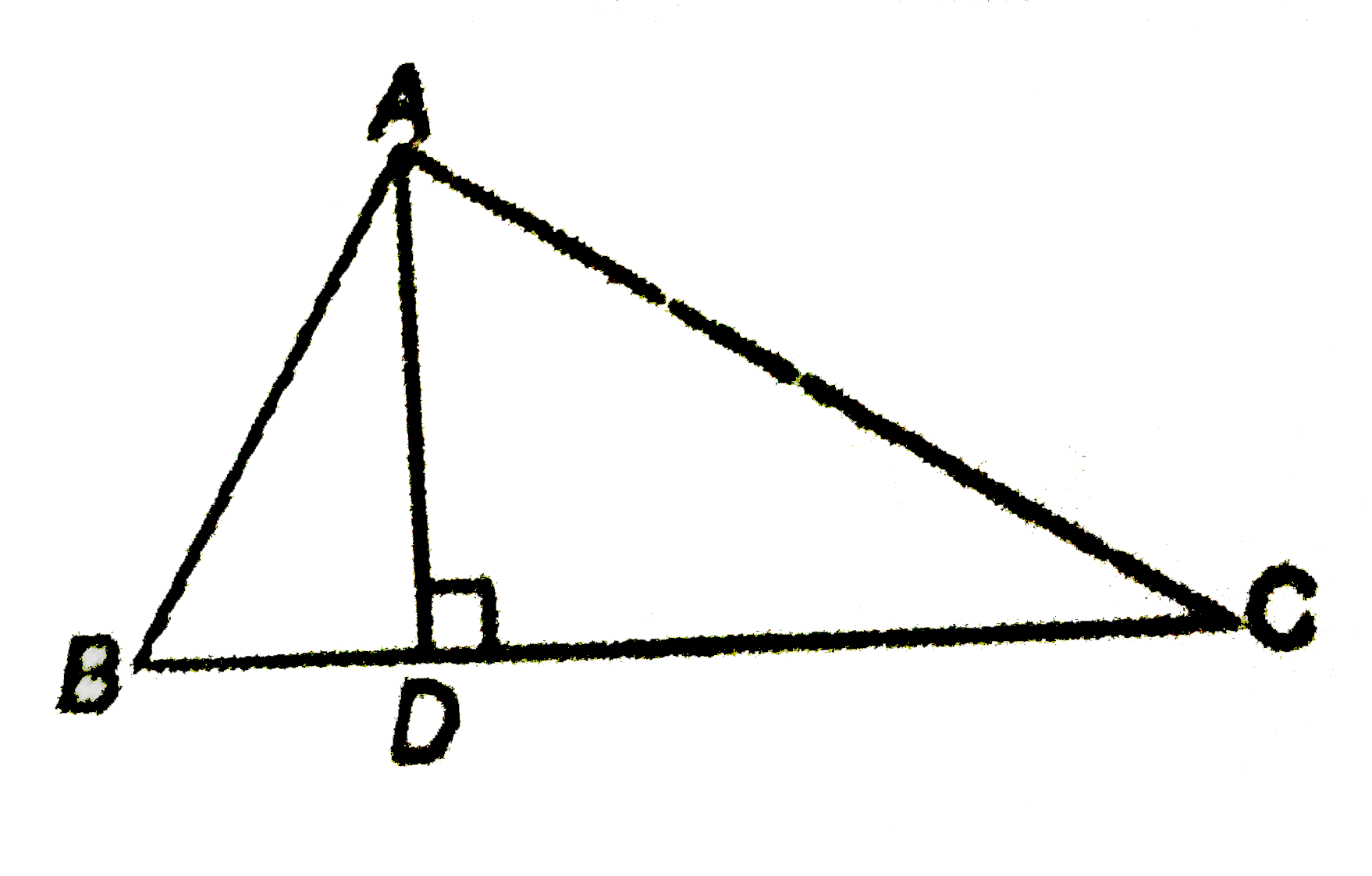
View SolutionThe perpendicular AD on the base BC of a ABC intersects BC at D so that DB=3CD . Prove that 2 AB2=2 AC2+BC2 .
View SolutionIn the given figure, ABCD is a quadrilateral in which AB∣∣DC and P is the midpoint of BC. On producing, AP and DC meet at Q. Prove that (i) AB=CQ, (ii) DQ=DC+AB
View Solution

