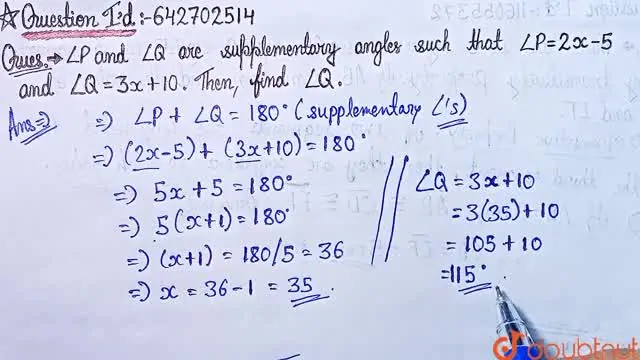∠P and ∠Q are supplementary angles such that ∠P=2x−5 and ∠Q=3x+10. Then, find ∠Q.
35∘
65∘
105∘
115∘
The correct Answer is:D
Step by step video, text & image solution for angleP and angleQ are supplementary angles such that angleP=2x-5 and angleQ=3x+10. Then, find angleQ. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Skill Testing Exercise21videos
LINE AND ANGLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS3videos
INTRODUCTION TO EUCLID.S GEOMETRY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Multiple Choice Questions (MCQs)10videos
PROBABILITY
Similar Questions
If ∠A and ∠B are supplementary angles, where ∠A=x+10∘ and ∠B=x−10∘, then find ∠A and ∠B.
View Solution∠P and ∠Q are supplementary angles. If ∠P=∠Q−40∘, then find ∠P and ∠Q.
View Solution∠Pand∠Q are two supplementary angles. If ∠P is three times of ∠Q, then find the measurement of the angles P and Q.
View SolutionIn ΔPQR,∠P=50∘and∠Q=60∘. Find angleR.
View SolutionTwo supplementary angles are in ratio 3:6. Find the angles
View SolutionTwo supplementary angles are in the ratio 2:3. Find the angles.
View SolutionTwo supplementary angles are in the ratio 4:5 . Find the angles.
View SolutionIf the supplementary angle of x is 4 times its complementary angle , then find x.
View SolutionTwo supplementary angles are in the ratio 2:3. The angles are
View SolutionIn an isosceles right triangle PQR, if ∠Q=90∘, then find ∠PRQ.
View Solution