A LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant ‘b’. If the amount of initial charge on the capacitor be Q0. then the amplitude of the amount of charge on the capacitor as a function of time t will be:
Q=Q0e−Rt2l
Q=Q0(1−e−2RtL)
Q=Q0e−RtL
Q=Q0(1−e−RtL)
The correct Answer is:A
For damped oscillation : ma+bv+kx=0
md2xdt2+bdxdt+kx=0 ….(i)
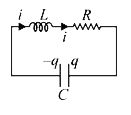
For LCR series circuit
−iR−Ldidt−qC=0
Ld2qdt2+Rdqdt+1Cq=0 …(ii)
Comparing (i) & (ii), L↔m,C↔1k,R↔b
Amplitude A=A0e−bt2m∴ Amplitude charge Q=Q0e−Rt2l
Similar Questions
Knowledge Check
An LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant b, the correct equivalence of b would be:
Ab↔RBb↔cCb↔1RDb↔1LAn LCR series circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring-mass damped oscillator having damping constant ‘b’, the correct equivalence would be (Take, i = current, V = voltage, x = displacement, q = charge, F = force, v = velocity)
Aq↔x,v<↔>i,F↔VBq↔v,i↔x,F↔VCq↔x,v↔V,F→iDq↔F,i↔x,V→vA LCR circuit be haves like a damped harmonic oscillator. The discharge of capacitor C, through an C□ inductor L having resistance R is oscillatory. Then which of following is correct _____.
A1LC<R24L2B1LC>R24L2C1LC>R34L4D1√LC>R38
A capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
View SolutionIn an oscillating LC circuit, L = 25.0 mH and C = 2.89 μF. At time t=0 the current is 9.20 mA, the charge on the capacitor is 3.80 μC and the capacitor is charging. What are (a) the total energy in the circuit, (b) the maximum charge on the capacitor, and (c) the maximum current? (d) If the charge on the capacitor is given by q= cos(ωt+ϕ), what is the phase angle ϕ? (e) Suppose the data are the same, except that the capacitor is discharging at t= 0. What then is ϕ ?
View SolutionA circuit with capacitance C and inductance L generates free damped oscillations with current varying with time as I=Ime−βtsinωt. Find the voltage across the capacitor as a function of time, and in particular, at the moment t=0.
View SolutionTime constant of a C-R circuit is 2ln(2) second. Capacitor is discharged at time t=0. The ratio of charge on the capacitor at time t=2s and t=6s is
View SolutionIf initial amplitude during a damped oscillation of mass m is 12 cm and after 2s it reduces to 6cm then find damping constant(b)
View Solution
