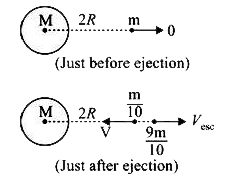
A satellite of mass m is launched vertically upwards with an initial speed √GM® from the surface of the earth. After it reaches height R (R = radius of the earth), it ejects a rocket of mass m10 in a direction opposite to the initial direction of the satellite, so that subsequently the satellite escapes to infinity. The minimum kinetic energy of the rocket at ejection needed is (G is the gravitational constant, M is the mass of the earth):
8140.GMmR
2120.GMmR
8110.GMmR
2140.GMmR
The correct Answer is:A
Energy conservation
−GMmR+12m(√GMR)2=−GMm2R+12mv21
v1=0
Momentum conservation:
0=9m10Vesc−m10V
V=9Vesc=9√GM2R
Kinetic energy of rocket =12.m10.81V2esc
=8140.GMmR
Similar Questions
A satellite of mass m0 is revolving around the earth in circular orbit at a height of 3R from surface of the earth the areal velocity of satellite is (where R is radius of earth and M0 is the mass of earth)
View SolutionA satellite of mass 'M' is projected radially from surface of earth with speed 'u'. When is reaches a height equal to radius of earth, it ejects a rocket of mass M10and it itself starts orbiting the earth in circular path of radius 2R, find the kinetic energy of rocket.
View Solution
Knowledge Check
A satellite of mass m is launched vertically upwards with an initial speed U from the surface of the Earth. After it reaches height 2 R (R = radius of Earth) it ejects a rocket of mass m5 So, that subsequently the satellite moves in a circular orbit. The kinetic energy of rocket is (M is mass of Earth)
Am10(25U2−84GM3R)Bm10(15U2−74GM3R)Cm8(U√10GM3R)Dm6(25U2−64GM3R)A satellite of mass m is launched vertically upwards with initial kinetic energy K from the Earth’s surface. After it reaches height R (R = radius of earth). It ejects a rocket of mass m5 so that subsequently the satellite moves in a circular orbit. The kinetic energy of rocket is [G is gravitational constant, M is the mass of the earth, take GMmR=K]
A5K2B66K5C33K10D10KA body is projected vertically upwards with a speed of √GMR ( M is mass and R is radius of earth ) . The body will attain a height of
AR2BRC54RD3R2
A satellite A of mass m is at a distance of r from the surface of the earth. Another satellite B of mass 2m is at a distance of 2r from the the earth's centre. Their time periods are in the ratio of
View SolutionA satellite of mass m is orbiting around the earth at a height h above the surface of the earth. Mass of the earth is M and its radius is R. The angular momentum of the satellite is independent of
View SolutionA satellite of mass m is orbiting around the earth at a height h above the surface of the earth. Mass of the earth is M and its radius is R. The angular momentum of the satellite is independent of :
View SolutionA satellite of mass m is orbiting around the earth at a height h above the surface of the earth. Mass of the earth is M and its radius is R. The angular momentum of the satellite is independent of
View SolutionA satellite of mass m revolves around the earth of radius R at a height x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View Solution
